Задание 23 из ОГЭ по математике: задача 40
Разбор сложных заданий в тг-канале:
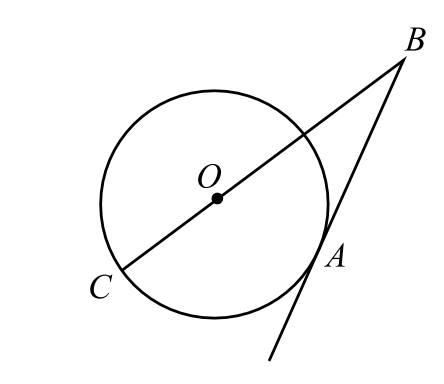
Найдите угол $ABO$, если его сторона $AB$ касается окружности с центром в точке $O$, а дуга $AC$, заключённая внутри этого угла, равна $120^°$
Объект авторского права ООО «Легион»
Посмотреть решение
Вместе с этой задачей также решают:
В прямоугольном треугольнике катет и гипотенуза равны соответственно 7 и 25. Найдите высоту, проведенную к гипотенузе, радиусы вписанной и описанной окружностей, площадь треугольни…
В трапеции $ABCD$ c основаниями $BC=20$ и $AD=70$ проведена прямая, параллельная основаниям трапеции и пересекающая боковые рёбра $AB$ и $CD$ соответственно в точках $E$ и $F$. Найдите $CF:FD$, ес…
Даны две параллельные прямые. На первой прямой взят отрезок AB, на второй – CD. Точка O – точка пересечения отрезков AD и BC. Известно, что AB=10, CD=20, AD=30. Найдите OD.
Онлайн-школа «Турбо»
- Прямая связь с преподавателем
- Письменные дз с проверкой
- Интересные онлайн-занятия
- Душевное комьюнити
Получить бесплатно
Популярные материалы
Составим твой персональный план подготовки к ОГЭ. Абсолютно бесплатно!
Хочу!
