Задание 12 из ЕГЭ по математике (база): задача 18

Разбор сложных заданий в тг-канале:

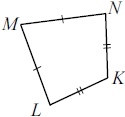
В выпуклом четырёхугольнике $LMNK$ известно, что $LM = MN, LK = KN, ∠M = 64°, ∠K = 122°$. Найдите угол $N$. Ответ дайте в градусах.

Объект авторского права ООО «Легион»

Посмотреть решение

Предыдущая задача

Следующая задача

Вместе с этой задачей также решают:

Стороны параллелограмма равны 16 и 20. Высота, опущенная на меньшую сторону, равна 15. Найдите длину высоты, опущенной на большую сторону параллелограмма.

Стороны параллелограмма равны 30 и 40. Высота, опущенная на меньшую сторону, равна 38. Найдите длину высоты, опущенной на большую сторону параллелограмма.

В треугольнике ABC известно, что AB = BC = 61, AC = 22. Найдите длину медианы.

В треугольнике ABC AC = 15, BF - медиана, BL - высота, BF = BC. Найдите длину отрезка AL.