Задание 16 из ОГЭ по математике: задача 16
Разбор сложных заданий в тг-канале:
Сложность: 
Среднее время решения: 1 мин. 9 сек.
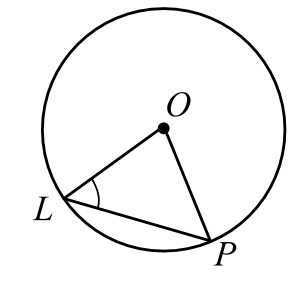
Центральный угол $LOP$ опирается на хорду $LP$ длиной $13$. При этом угол $OLP$ равен $60^°$ (см. рис.). Найдите радиус окружности.
Объект авторского права ООО «Легион»
Посмотреть решение
Вместе с этой задачей также решают:
Два угла вписанного в окружность четырёхугольника равны $75^°$ и $92^°$ (см. рис.). Найдите меньший из оставшихся углов. Ответ дайте в градусах.
Четырёхугольник $ABCD$ вписан в окружность, причём угол $B$ равен $87^°$ (см. рис.). Найдите угол $D$. Ответ дайте в градусах.
Онлайн-школа «Турбо»
- Прямая связь с преподавателем
- Письменные дз с проверкой
- Интересные онлайн-занятия
- Душевное комьюнити
Получить бесплатно
Популярные материалы
Составим твой персональный план подготовки к ОГЭ. Абсолютно бесплатно!
Хочу!
