Окружность
Окружностью называется геометрическое место точек плоскости, равноудалённых от данной точки, называемой центром окружности.
Основные свойства окружности
1. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
2. Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
3. Серединный перпендикуляр к хорде проходит через центр окружности.
4. Равные хорды удалены от центра окружности на равные расстояния.
5. Хорды окружности, удалённые от центра на равные расстояния, равны.
6. Окружность симметрична относительно любого своего диаметра.
7. Дуги окружности, заключённые между параллельными хордами, равны.
8. Из двух хорд больше та, которая менее удалена от центра.
9. Диаметр есть наибольшая хорда окружности.
Замечательные свойства окружности
1. Геометрическое место точек M, из которых отрезок AB виден под прямым углом (∠AMB = 90°), есть окружность с диаметром AB без точек A и B
2. Геометрическое место точек M, из которых отрезок AB виден под острым углом (∠AMB < 90°), есть внешность круга с диаметром AB без точек прямой AB.
3. Геометрическое место точек M, из которых отрезок AB виден под тупым углом (∠AMB > 90°), есть внутренность круга с диаметром AB без точек отрезка AB
4. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (без концов этих дуг).
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
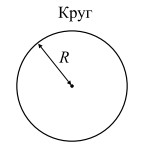 |
R — радиус; l — длина окружности |
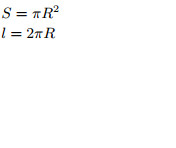 |
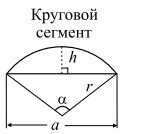 |
r — внутренний радиус; R — наружный радиус; d — внутренний диаметр; D — наружный диаметр; 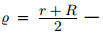 средний радиус; δ = R − r — ширина кольца; α — центральный угол части кольца (в градусах). |
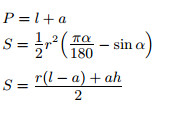 |
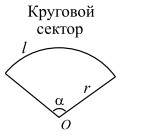 |
r — радиус; α — центральный угол (в градусах); 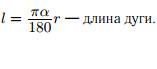
|
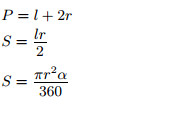 |
Площади круга и сектора
Площадь круга равна произведению числа π на квадрат радиуса:S = πR2.
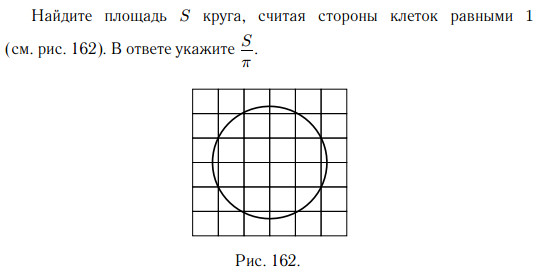
Решение.
Площадь круга равна произведению числа π на квадрат радиуса. Найдём радиус. Из центра O проведём радиус OA. В треугольнике OAB сторона OA — гипотенуза, катеты равны 1 и 2 (см. рис. 163)
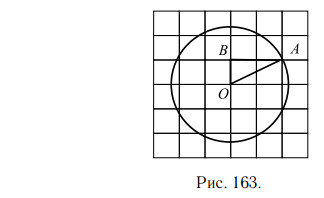
Найдём гипотенузу по теореме Пифагора.

Ответ: 5
На клетчатой бумаге нарисовано два круга (см. рис. 164). Площадь внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.
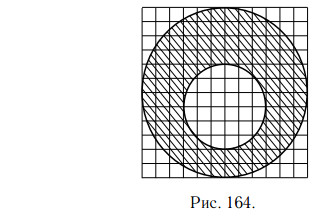
Решение.
Радиус R внутреннего круга — 3 клетки, его площадь равна πR2 = 3. Радиус внешнего круга — 6 клеток, то есть 2R, поэтому его площадь равна π · (2R)2 = 3 · 4 = 12. Площадь заштрихованной фигуры равна разности 12 − 3 = 9.
Ответ: 9






