Виды и свойства линз. Построение изображения в линзах

Линзы. Фокусное расстояние и оптическая сила линзы

Линза (нем. linse произошло от лат. lens — чечевица) — это простейший оптический элемент, ограниченный с двух сторон сферическими поверхностями.

Обычно линзы изготавливаются из оптического стекла (стекло специального изготовления с минимальным количеством дефектов: пузырьков воздуха, включений посторонних микрочастиц).

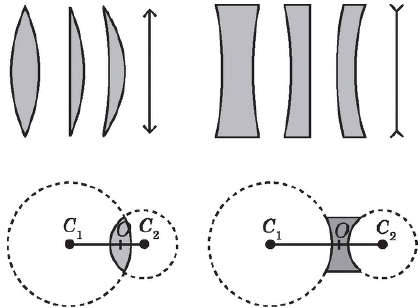
Линзы бывают выпуклые и вогнутые. У выпуклых линз середина толще, чем края, у вогнутых — наоборот. В свою очередь, выпуклые линзы делятся на двояковыпуклые, плосковыпуклые ивогнуто-выпуклые. Вогнутые линзы делятся на двояковогнутые, плосковогнутые и выпукло-вогнутые. На рисунке рядом с изображениями линз (справа) даны их условные обозначения на оптических схемах.

Тонкая линза. Если толщина линзы пренебрежимо мала по сравнению с радиусами кривизны ее поверхностей и расстоянием от предмета до линзы, ее называют тонкой линзой. Вершины сферических сегментов тонкой линзы расположены так близко, что их принимают за одну точку, называемую центром линзы, и обозначают буквой $О$. Луч света, проходящий через оптический центр линзы, практически не преломляется.

Прямая $С_1С_2$, проходящая через центры сферических поверхностей $О$, ограничивающих линзу, называется главной оптической осью линзы. Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью.

Фокусы линзы

Выпуклая (положительная, или собирающая) линза. Если на выпуклую линзу направить пучок света параллельно ее главной оптической оси, то после преломления в линзе он соберется в некоторой точке $F$ на оси линзы, которая называется главным фокусом линзы. Поэтому такие линзы называются положительными, или собирающими. Расстояние от центра линзы $О$ до точки $F$ называется фокусным расстоянием линзы. У линзы имеется два главных фокуса, с каждой стороны по одному.

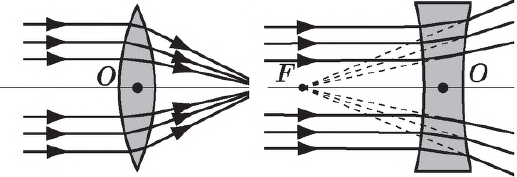
Вогнутая (отрицательная, или рассеивающая) линза. Пучок света, направленный параллельно оптической оси вогнутой линзы, после преломления в ней расходится. Если эти расходящиеся лучи продолжить в обратную сторону, они соберутся на оптической оси линзы со стороны падающего пучка в точку, которая называется мнимым фокусом линзы. Глазу, расположенному с правой стороны, будет казаться, что пучок лучей исходит из точки $F$. Такая линза называется отрицательной, или рассеивающей. Как и в случае собирающей линзы, фокусное расстояние измеряется от оптического центра до фокуса.

Фокусное расстояние линзы зависит от кривизны поверхностей, ограничивающих линзу. Чем больше кривизна поверхности линзы, тем меньше фокусное расстояние.

Оптическая сила линзы

Оптической силой линзы называется физическая величина, обратная фокусному расстоянию:

$D={1}/{F}$

Оптическая сила измеряется в диоптриях (дптр). В СИ единицей оптической силы является метр в минус первой степени ($м^{-1}$).

Фокусное расстояние собирающей линзы (и соответственно, ее оптическую силу) условились считать положительной величиной, т. к. собирающая линза обладает действительным фокусом.

Фокусное расстояние рассеивающей линзы (и, соответственно, ее оптическая сила) — отрицательная величина, т. к. у рассевающей линзы мнимый фокус.

Построение изображений в линзах

Любой предмет можно разбить на маленькие области, которые условно могут быть приняты за точки. Поэтому для построения изображения любого предмета необходимо знать, как строится изображение произвольной точки.

Собирающая линза

Для образования оптического изображения точки в линзе достаточно двух лучей. В качестве таковых выбираются любые два из трех лучей, ход которых известен: 1) луч, идущий параллельно оптической оси линзы — луч $АС$, который после преломления пересекает оптическую ось в фокусе линзы $F$; 2) луч, проходящий через оптический центр линзы, который не меняет своего направления (луч $АА_1$); 3) луч, проходящий через фокус линзы, который после преломления пойдет параллельно главной оптической оси — луч $АD$. Точка $А_1$ пересечения этих трех лучей за линзой и будет изображением исходной точки $А$.

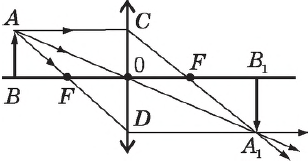
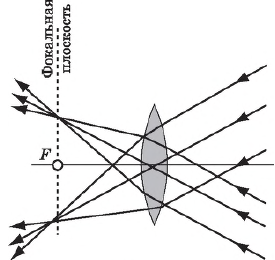
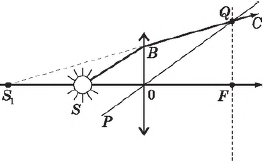
Для построения изображения точки $S$, находящейся на главной оптической оси, все три упомянутых выше луча не подходят, т. к. сливаются в один, идущий вдоль главной оптической оси, и потому в этом случае пользуются следующим приемом. Из точки $S$ проводят произвольный луч $SB$ до пересечения с линзой. Чтобы найти ход этого луча после преломления в линзе, проводят через центр линзы $О$ луч, параллельный $SB$ и являющийся побочной оптической осью линзы, до пересечения с фокальной плоскостью линзы в точке $Q$. Через эту точку пройдет преломленный луч $ВС$. Таким образом построен ход лучей, выходящих из точки $S$. После преломления эти лучи расходятся. Изображение $S_1$ будет мнимым, т. к. источник расположен между главным фокусом и линзой.

Рассеивающая линза

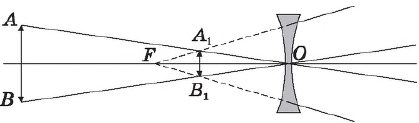
Построение изображения в рассеивающей линзе показано на рисунке. Поскольку лучи после преломления в рассеивающей линзе не пересекаются, то в фокусе ее собираются продолжения этих лучей. Получаемое изображение, следовательно, является мнимым и прямым. Изображение предмета расположено всегда между фокусом и оптическим центром линзы и поэтому оно всегда уменьшенное.

Формула тонкой линзы

Используя законы геометрии, в частности, подобие треугольников, можно вывести формулу, связывающую расстояние $d$ от предмета до линзы, расстояние $d_1$ от изображения до линзы и фокусное расстояние линзы $f$:

${1}/{d}+{1}/{d_1}={1}/{f}$

или

${1}/{d}+{1}/{d_1}=D$

Уравнения называют формулой тонкой линзы. Величины, входящие в формулу, могут быть как положительными, так и отрицательными. Фокусное расстояние $f$ собирающей линзы считается положительным, а рассеивающей — отрицательным. Расстояние $d$ от линзы до предмета положительно, если это действительная светящаяся точка, и отрицательно, если мнимая (т. е. если на линзу падает сходящийся пучок лучей, продолжение которых сходится в одной точке). Расстояние $d_1$ от изображения до линзы положительно, если изображение действительное, и отрицательно, если оно мнимое. Учитывая сказанное, перед каждым членом в формулах ставят знак «+» или «-». Если знаки величин, входящих в формулы, неизвестны, ставят «+». Если в результате вычислений у какой-либо из величин получается знак «-», значит, эта величина — мнимая.

Увеличение линзы

Линейным увеличением $Г$ линзы называется отношение линейного размера изображения $H$ к линейному размеру предмета $h$: $Г={H}/{h}$

Увеличение линзы равно отношению расстояния от изображения до линзы к расстоянию от линзы до предмета:

$Г={|d_1|}/{|d|}$

Линзы являются основной частью фотоаппарата, проекционного аппарата, микроскопа и телескопа. В глазу есть своя линза — хрусталик.