Геометрическая оптика: отражение и преломление света. Тень и полутень

Закон отражения света

Принцип Гюйгенса. Принцип Гюйгенса—Френеля

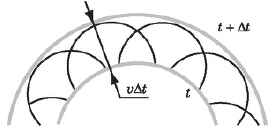
Для того чтобы, зная положение волновой поверхности в момент времени $t$, найти ее положение в следующий момент времени $t+∆t$, нужно каждую точку волновой поверхности рассматривать как источник вторичных волн. Поверхность, касательная ко всем вторичным волнам, представляет собой волновую поверхность в следующий момент времени. Этот принцип справедлив для распространения волн любой природы, хотя Гюйгенсом он был сформулирован именно для световых волн.

Для механических волн принцип Гюйгенса имеет наглядное истолкование: частицы среды, до которых доходят колебания, в свою очередь, колеблясь, приводят в движение соседние частицы среды, с которыми они взаимодействуют.

Принцип Гюйгенса—Френеля — основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности световых.

Принцип Гюйгенса—Френеля является развитием принципа, который ввел современник Ньютона X. Гюйгенс в 1678 г.

О. Френель объединил принцип Гюйгенса с идеей интерференции вторичных волн. Согласно идее Френеля, волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.

Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света сферической поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.

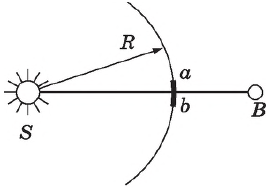
Такого рода расчеты показали, что результат интерференции вторичных волн в точке $B$ от источников, расположенных на сферической поверхности радиуса $R$, оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте $ab$ посылали свет в точку $B$. Вторичные волны, испускаемые источниками, расположенными на остальной части поверхности, гасят друг друга в результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой $SB$, то есть прямолинейно.

Отражение света. Закон отражения света

Большинство окружающих нас предметов видимы глазу не потому, что излучают свет, а потому, что отражают его.

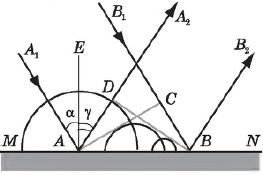
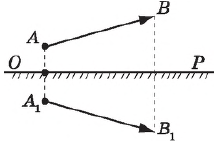
Закон отражения света. Пусть на зеркальную поверхность $MN$ падает луч света $А_1А$. Луч $А_1А$ называется падающим лучом, точка $А$ пересечения этого луча с поверхностью называется точкой падения. Восстановим из точки $А$ перпендикуляр $АЕ$ к поверхности $МN$. Угол $α$ между падающим лучом и перпендикуляром называется углом падения. Пусть луч $А_1А$, отразившись от поверхности, распространяется в направлении $АА_2$ под некоторым углом $γ$. Луч $АА_2$ называется отраженным лучом, а угол $γ$ — углом отражения. Плоскость, в которой лежат луч $А_1А$ и перпендикуляр $АЕ$, называется плоскостью падения.

Закон отражения света гласит:

1. Отраженный луч лежит в плоскости падения.
2. Угол падения равен углу отражения ($α=γ$).

Обратимость направления световых лучей. Если падающий луч направить вдоль $А_2А$, то он отразится вдоль направления $АА_1$. В этом заключается принцип обратимости хода лучей света. Он также является одним из основных положений геометрической оптики и используется при построении оптических изображений.

Закон отражения можно вывести с помощью принципа Гюйгенса.

Пусть плоская волна, обозначенная лучами $А_1А$ и $В_1В$ и плоской волновой поверхностью $АС$, падает на зеркальную плоскость $МN$ под некоторым углом $α$. Различные участки волновой поверхности $АС$ достигают отражающей границы не одновременно. Возбуждение колебаний в точке $А$ начнется на время $∆t={CB}/{υ}$ (где $υ$ — скорость волны) раньше, чем в точке $В$.

В момент, когда волна достигнет точки $В$ и в этой точке начнется возбуждение колебаний, вторичная волна с центром в точке $А$ будет представлять собой полусферу радиусом $r=AD=υ∆t=CB$. Изменение радиусов вторичных волн от точек, лежащих между точками $А$ и $В$. Плоскость $DB$ — огибающая вторичных волн, касательная к сферическим поверхностям. $DB$ — волновая поверхность отраженной волны. Отраженные лучи $АА_2$ и $ВВ_2$ перпендикулярны волновой поверхности $DB$; $γ$ — угол отражения.

Так как $AD=CB$ и треугольники $ADB$ и $АСВ$ прямоугольные, то $∠DBA=∠CAB$. Но $α=∠CAB$ и $γ=∠DBA$ как углы с перпендикулярными сторонами. Следовательно, угол отражения равен углу падения:

$α=γ$

Кроме того, из построения Гюйгенса вытекает, что падающий луч, луч отраженный и перпендикуляр, восстановленный в точке падения, лежат в одной плоскости, что и требовалось доказать.

Построение изображений в плоском зеркале

Оптическое изображение

Оптическое изображение — это картина, получаемая в результате прохождения через оптическую систему лучей, распространяющихся от объекта, и воспроизводящая его контуры и детали.

Под оптической системой понимают совокупность оптических деталей — линз, призм, зеркал, плоскопараллельных пластинок, скомбинированных определенным образом для получения оптического изображения или для преобразования светового потока, идущего от источника света.

Оптический объект (предмет, который мы хотим изобразить с помощью оптической системы) представляет собой совокупность точек, светящихся собственным светом (т. е. излучающих) либо отраженным светом.

Для того, чтобы изображение максимально соответствовало объекту (было качественным), необходимо, чтобы лучи света, исходящие из какой-либо точки объекта, после преломлений и отражений в оптической системе вновь сходились в одной точке, которая и является изображением точки объекта. Это возможно лишь тогда, когда точка объекта находится на небольшом расстоянии от оси оптической системы, например, линзы, так, что лучи, исходящие из предмета и участвующие в его изображении, находятся в так называемой параксиальной (приосевой) области оптической системы. Оптическая система, в которой точка изображается точкой, т. е. без искажений, и все пропорции предмета передаются правильно, называется идеальной оптической системой.

Применение законов геометрической оптики дает возможность получить изображение любой точки, находящейся в параксиальной области, без искажений.

Оптические изображения делятся на действительные и мнимые.

Под действительным изображением понимают такое, которое получается в результате пересечения реальных (действительных) лучей, вышедших из оптической системы (т. е. сходящихся лучей, пересекающихся в точке изображения). Примером такого изображения является изображение, получающееся на фотопленке.

Мнимым изображением называется изображение, получающееся в результате воображаемого пересечения расходящихся лучей, вышедших из оптической системы. Такое изображение нельзя получить на экране либо фотопленке. Глаз, тем не менее, увидит его в месте мнимого пересечения лучей. Мнимое изображение может служить источником света для дальнейшего построения действительного изображения другой оптической системой, которое затем можно зафиксировать, например, на фотопленке.

Примером мнимого изображения является всем знакомое изображение предметов в зеркале.

Построение изображения в плоском зеркале

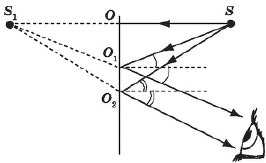
Пусть на плоское зеркало падает пучок лучей $SO, SO_1; SO_2$ из точечного источника $S$. После отражения в зеркале в глаз человека попадает расходящийся пучок лучей. Если теперь продолжить каждый из отраженных лучей за зеркало, то они пересекутся в одной точке $S_1$; которая и является мнимым изображением точки $S$. То, что лучи действительно пересекутся в одной точке, легко доказать, используя закон отражения света и теоремы геометрии, как и то, что $S_1O=SO, S_1O_2=SO_2, S_1O_3=SO_3$.

Отсюда следует, что правила построения предмета в зеркале сводятся к следующему: из точки $А$ предмета (в данном случае это стрелка $АВ$) опускают перпендикуляр на плоскость зеркала; на продолжении этого перпендикуляра за зеркалом на точно таком же расстоянии откладывают точку $А_1$; точно так же поступают с точкой $В$. Затем соединяют точки $А_1$ и $В_1$. Стрелка $А_1В_1$ и будет мнимым изображением стрелки $АВ$.

Из вышеизложенного следует, что изображение предмета в плоском зеркале симметрично предмету относительно плоскости зеркала. Последнее означает, что оно является мнимым, прямым (т. е. не перевернутым), равным по размеру самому предмету и находится на таком же расстоянии за зеркалом, на каком предмет расположен перед ним.

Закон преломления света

Преломление света — это изменение направления распространения светового луча при его прохождении через границу раздела двух прозрачных сред.

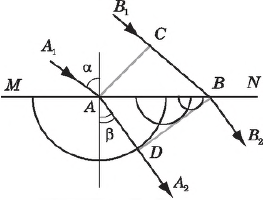
Луч $А_1А$, падающий на границу раздела $МN$ двух однородных сред; преломленный луч $АА_2$; перпендикуляр к плоскости раздела, проходящий через точку падения луча $А$. Угол $α$ называется углом падения, угол $β$ — углом преломления. Преломление света подчиняется определенным законам.

1. Луч падающий и луч преломленный лежат в одной плоскости с нормалью, проведенной к границе раздела двух сред в точке падения луча. Плоскость эта называется плоскостью падения.

2. Угол падения и угол преломления связаны соотношением:

${sinα}/{sinβ}=n$

где $n$ — постоянная, не зависящая от углов $α$ и $β$.

Величина п называется показателем преломления и зависит лишь от свойств обеих сред, через границу раздела которых проходит свет.

Закон преломления, выраженный соотношением ${sinα}/{sinβ}=n$, называется законом Спелля (Снеллиуса).

Закон преломления света выводится с помощью принципа Гюйгенса. Преломление света при переходе из одной среды в другую вызвано различием в скоростях распространения света в этих средах. Пусть плоская волна, обозначенная лучами $А_1А$ и $В_1В$ и плоской волновой поверхностью $AС$, падает на зеркальную плоскость $МN$ под некоторым углом $α$. Различные участки волновой поверхности $АС$ достигают отражающей границы не одновременно. Возбуждение колебаний в точке $А$ начнется на время $∆t={CB}/{υ_1}$ (где $υ_1$ — скорость волны в первой среде) раньше, чем в точке $В$. В момент времени, когда вторичная волна в точке $В$ только начнет возбуждаться, волна от точки $А$ во второй среде уже имеет вид полусферы радиусом $AD=υ_2·∆t$, где $υ_2$ — скорость света во второй среде. Волновая поверхность преломленной волны (от центров, лежащих на границе раздела двух сред) в этот момент времени представлена плоскостью $BD$ — касательной к волновым поверхностям всех вторичных волн во второй среде.

Угол падения $α$ луча равен $∠CAB$ в треугольнике $АВС$ (стороны одного угла перпендикулярны сторонам другого). Следовательно,

$CB=υ_1∆t=ABsinα$

Угол преломления $β$ равен углу $ABD$ треугольника $ABD$. Поэтому

$AD=υ_2∆t=ABsinβ$

Разделив почленно $R_n=R+r_1+r_2+r_3$ на $I=I_1+I_2$, получим

${sinα}/{sinβ}={υ_1}/{υ_2}=n$

где $n$ — постоянная величина, не зависящая от угла падения.

Из построения видно, что луч падающий и луч преломленный лежат в одной плоскости с нормалью, проведенной к границе раздела двух сред в точке падения луча. Это утверждение вместе с выражением $U=U_1=U_2$ представляет собой закон преломления света.

Таким образом, из принципа Гюйгенса не только выводится закон преломления света, но и раскрывается физический смысл показателя преломления: он равен соотношению скоростей света в средах, на границе между которыми происходит преломление.

Абсолютный и относительный показатели преломления

Показатель преломления (коэффициент преломления) — это оптическая характеристика среды, связанная с преломлением света на границе раздела двух прозрачных, оптически однородных и изотропных сред при переходе из одной среды в другую и связанная с различием скоростей распространения света $υ_1$ и $υ_2$ в этих средах.

Величина показателя преломления, равная соотношению этих скоростей $n_{21}={υ_1}/{υ_2}$, называется относительным показателем преломления. Если свет падает на первую или вторую среду из вакуума, где скорость распространения света равна $с$, то показатель преломления называется абсолютным показателем преломления и равен $n_1={c}/{υ_1}$ или $n_2={c}/{υ_2}$ соответственно. Относительный показатель преломления при переходе из первой среды во вторую связан с абсолютными показателями преломления этих сред соотношением $n_{21}={n_2}/{n_1}$, и закон преломления ${sinα}/{sinβ}=n$ может быть записан в виде

$n_{1}sinα=n_{2}sinβ$

где $α$ и $β$ — углы падения и преломления соответственно.

Среда, в которой скорость света больше, называется оптически менее плотной. Таким образом, при переходе из оптически менее плотной среды в оптически более плотную $n > 1$, т. е. угол преломления меньше угла падения, и наоборот.

Абсолютный показатель преломления зависит от природы и строения вещества, его агрегатного состояния, температуры, давления, наличия в нем упругих напряжений. Показатель преломления данной среды зависит от длины волны света.

Изложенные выше закономерности поведения света на границе двух сред относятся к монохроматическому свету (свету одной определенной частоты, или одного цвета). Было установлено, что частота электромагнитных колебаний при прохождении волны из первой среды во вторую, остается неизменной: $ν_1=ν_2$, а вот скорость распространения волны меняется, что и означает изменение показателя преломления. В более плотных средах скорость света меньше, чем в менее плотных, а абсолютный показатель преломления — больше. Поскольку частота, скорость и длина волны связаны известным соотношением, то с учетом вышесказанного легко показать, что

$n_{1}λ_1=n_{2}λ_2$

где $λ_1$ и $λ_2$ — длины волн света в средах $1$ и $2$ соответственно.

Зависимость показателя преломления от цвета (длины волны) называется дисперсией. Подробнее о ней будет сказано далее.

Для большинства прозрачных жидкостей и твердых тел показатель преломления в видимой области в среднем равен $1.5$. Абсолютный показатель преломления воздуха для желтого света при нормальных условиях равен $∼1.000292$. Поэтому показатели преломления различных веществ рассматривают относительно воздуха.