Электромагнитные колебания и волны
Свободные электромагнитные колебания в колебательном контуре
Колебательный контур — это электрическая цепь, содержащая индуктивность $L$, емкость $С$ и сопротивление $R$, в которой могут возбуждаться электрические колебания.
Колебательный контур — один из основных элементов радиотехнических систем. Различают линейные и нелинейные колебательные контуры. Параметры $R, L$ и $С$ линейного колебательного контура не зависят от интенсивности колебаний, а период колебаний не зависит от амплитуды.
При отсутствии потерь ($R = 0$) в линейном колебательном контуре происходят свободные гармонические колебания.
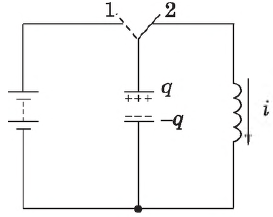
Для возбуждения колебаний в контуре конденсатор предварительно заряжают от батареи аккумуляторов, сообщив ему энергию $W_р$ и переводят переключатель в положение $2$. После замыкания цепи конденсатор начнет разряжаться через катушку индуктивности, теряя энергию. В цепи появится ток, вызывающий переменное магнитное поле. Переменное магнитное поле, в свою очередь приводит к созданию вихревого электрического поля, препятствующего току, в результате чего изменение тока происходит постепенно. По мере увеличения тока через катушку возрастает энергия магнитного поля $W_M$. Полная энергия $W$ электромагнитного поля контура остается постоянной (при отсутствии сопротивления) и равной сумме энергий магнитного и электрического полей. Полная энергия, в силу закона сохранения энергии, равна максимальной энергии электрического или магнитного поля:
$W={LI^2}/{2}+{q^2}/{2C}={q_m^2}/{2C}={LI_m^2}/{2}$
где $L$ — индуктивность катушки, $I$ и $I_m$ — сила тока и ее максимальное значение, $q$ и $q_m$ — заряд конденсатора и его максимальное значение, $C$ — емкость конденсатора.
Процесс перекачки энергии в колебательном контуре между электрическим полем конденсатора при его разрядке и магнитным полем, сосредоточенным в катушке, полностью аналогичен процессу превращения потенциальной энергии растянутой пружины или поднятого груза математического маятника в кинетическую энергию при механических колебаниях последних.
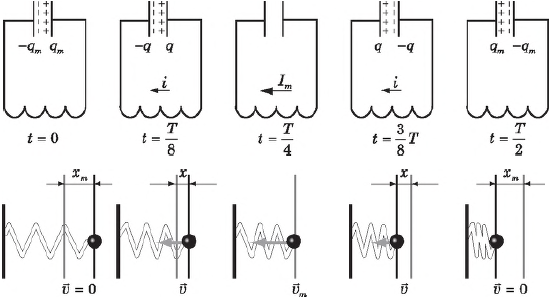
В таблице приводится соответствие между механическими и электрическими величинами при колебательных процессах.
Соответствие между механическими и электрическими величинами при колебательных процессах
| Механические величины | Электрические величины |
| Координата $х$ Скорость $υ$ Масса $m$ Жесткость пружины $k$ Потенциальная энергия $kх^2$/$2$ Кинетическая энергия $m^2$/$2$ |
Заряд $q$ Сила тока $i$ Индуктивность $L$ Величина, обратная емкости $1$/$С$ Энергия электрического поля $q^2$/$(2С)$ Энергия магнитного поля $Li^2$/$2$ |
Дифференциальное уравнение, описывающее процессы в колебательном контуре, можно получить, приравняв производную по полной энергии контура к нулю (поскольку полная энергия постоянна) и заменив в полученном уравнении ток на производную заряда по времени. В окончательном виде уравнение выглядит так:
$q''=-{1}/{LC}q$
Как видно, уравнение ничем не отличается по форме от соответствующего дифференциального уравнения для свободных механических колебаний шарика на пружине. Заменив механические параметры системы на электрические с помощью приведенной выше таблицы, мы в точности получим уравнение.
По аналогии с решением дифференциального уравнения для механической колебательной системы циклическая частота свободных электрических колебаний равна:
$ω_0={1}/{√{LC}}$
Период свободных колебаний в контуре равен:
$T={2π}/{ω_0}=2π√{LC}$
Формула $T={2π}/{ω_0}=2π√{LC}$ называется формулой Томсона в честь английского физика У. Томсона (Кельвина), который ее вывел.
Увеличение периода свободных колебаний с возрастанием $L$ и $С$ объясняется тем, что при увеличении индуктивности ток медленнее нарастает и медленнее падает до нуля, а чем больше емкость, тем больше времени требуется для перезарядки конденсатора.
Гармонические колебания заряда и тока описываются теми же уравнениями, что и их механические аналоги:
$q=q_{m}cosω_0t$
$i=q'=-ω_{0}q_{m}sinω_0t=I_{m}cos(ω_0t+{π}/{2})$
где $q_m$ — амплитуда колебаний заряда, $I_m=ω_0q_m$ — амплитуда колебаний силы тока. Колебания силы тока опережают по фазе на ${π}/{2}$ колебания заряда.





