Электромагнитная индукция. Закон Фарадея. Правило Ленца

Электромагнитная индукция

Магнитный поток

Под магнитным потоком понимают поток $Ф$ вектора магнитной индукции $B↖{→}$ через какую-либо поверхность $S$.

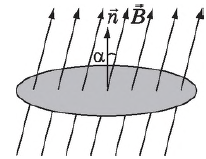
Магнитный поток $Ф$, пронизывающий контур, равен произведению модуля вектора индукции магнитного поля $В↖{→}$ на площадь $S$, ограниченную этим контуром, и на косинус угла а между нормалью к плоскости контура $n↖{→}$ и вектором $B↖{→}$.

$Ф=BScosα$

Произведение $Bcosα=B_n$ является проекцией вектора магнитной индукции на нормаль к плоскости контура, поэтому

$Ф=B_{n}S$

Магнитный поток пропорционален числу линий магнитной индукции, пронизывающих поверхность контура, и характеризует распределение магнитного поля на поверхности, ограниченной замкнутым контуром.

Единицей магнитного потока в СИ является вебер (Вб). Магнитный поток в $1$ Вб создается однородным магнитным полем с индукцией $1$ Тл через поверхность площадью $1$ м², расположенную перпендикулярно вектору магнитной индукции.

Закон электромагнитной индукции Фарадея

М. Фарадеем было установлено, что сила индукционного тока пропорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:

$I_i∼{∆Ф}/{∆t}$

Возникновение тока в замкнутом контуре означает наличие сторонних сил, работа которых по перемещению единичного заряда в контуре называется электродвижущей силой (ЭДС). Это означает, что при изменении потока через поверхность, ограниченную замкнутым контуром, в контуре возникает ЭДС $ε_1$ которую называют ЭДС индукции. Согласно закону Ома для замкнутой цепи, $I_i={ε_i}/{R}$.

Следовательно, ЭДС индукции пропорциональна ${∆Ф}/{∆t}$, поскольку сопротивление $R$ не зависит от изменения магнитного потока.

Закон электромагнитной индукции формулируется так:

ЭДС индукции $ε_1$ в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, ограниченную контуром:

$ε_1=|{∆Ф}/{∆t}|$

Применение правила Ленца к замкнутому контуру с положительной нормалью приводит к выражению:

$ε_1=-{∆Ф}/{∆t}$

Формула $ε_1=-{∆Ф}/{∆t}$ выражает основной закон электромагнитной индукции.

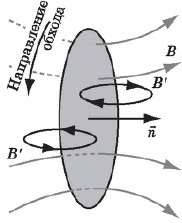
На рис. внешнее магнитное поле индукции $В$ возрастает со временем и направлено вдоль положительной нормали к контуру с током.

Индуцированный ток противоположен выбранному направлению обхода в соответствии с индуцированным магнитным полем $В'$.

Описанные выше опыты свидетельствуют о том, что электромагнитная индукция — это возникновение электрического поля и электрического тока при изменении во времени магнитного поля или при движении проводника в магнитном поле. Эти два типа эффектов электромагнитной индукции отличаются физической природой процессов, отвечающих за их возникновение. Первый тип обусловлен наведением вихревого электрического поля переменным магнитным полем, второй — действием сил Лоренца на движущиеся заряды в стационарном магнитном поле. В обоих случаях выполняется основной закон индукции, выраженный формулой $ε_1=-{∆Ф}/{∆t}$.

Вихревое электрическое поле

В первом типе электромагнитной индукции ЭДС возникает в неподвижном замкнутом проводнике при любом изменении магнитного поля.

С другой стороны, известно, что возникновение электродвижущей силы в любой цепи связано со сторонними силами, действующими на заряды в этой цепи. Под сторонними силами имеются в виду силы неэлектростатического характера. Какова же природа этих сил в данном случае?

Результаты различных экспериментов по электромагнитной индукции показали, что ЭДС индукции не зависит ни от материала проводника (металл, электролит и т. д.), ни от его состояния (например, величины и распределения температуры). Отсюда следует вывод, что сторонние силы связаны с самим магнитным полем.

Анализ явления электромагнитной индукции привел Дж. Максвелла к заключению, что причиной появления ЭДС индукции является электрическое поле, отличающееся от электростатического поля следующими особенностями.

1. Возникновение поля никак не связано с наличием проводников; оно существует в пространстве, окружающем переменное магнитное поле, независимо от наличия в нем проводников; проводники являются лишь индикаторами поля (если проводник замкнут, по нему течет ток).

2. Это поле не является электростатическим, поскольку силовые линии электростатического поля всегда разомкнуты, они начинаются и заканчиваются на зарядах, и напряжение по замкнутому контуру в электростатическом поле равно нулю; электростатическое поле не может поддерживать движение зарядов в замкнутом контуре, т. е. привести к возникновению ЭДС.

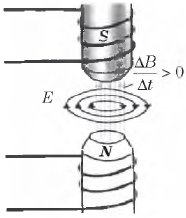
3. В противоположность последнему индуцированное переменным магнитным полем электрическое поле является вихревым (как и магнитное поле); оно имеет замкнутые силовые линии, приводит к возникновению ЭДС индукции, приводящей в движение заряды по замкнутым проводам.

4. В отличие от электростатического поля, работа сил вихревого электрического поля и электрическое напряжение по замкнутому контуру не равны нулю, а значение напряжения между двумя точками определяется не только их взаимным положением, но и формой контура, соединяющего эти точки.

Все вышеизложенное позволяет сделать вывод, который выражает первое основное положение теории Максвелла: любое изменение магнитного поля вызывает появление вихревого электрического поля.

Направление силовых линий напряженности $Е↖{→}$ совпадает с направлением индукционного тока. Работа вихревого электрического поля при перемещении единичного положительного заряда вдоль замкнутого неподвижного проводника численно равна ЭДС индукции в этом проводнике. Чем быстрее меняется индукция магнитного поля, тем больше напряженность индуцированного электрического поля.

Вихревые токи (токи Фуко). В массивном проводнике, находящемся в переменном магнитном поле, вихревое электрическое поле вызывает индукционный ток. Поскольку линии напряженности $Е↖{→}$ замкнуты, то и линии тока внутри этого массивного проводника замкнуты, поэтому они называются вихревыми токами, или токами Фуко. В 1855 г. Ж. Б. Л. Фуко обнаружил нагревание ферромагнитных сердечников, а также других металлических тел в переменном магнитном поле. Он объяснил этот эффект возбуждением индукционных токов. Фуко предложил способ уменьшения потерь энергии за счет нагрева — изготавливать сердечники и другие магнитопроводы в виде пластин, разделенных тонкими изолирующими пленками, и ориентировать поверхности этих пластин перпендикулярно вектору напряженности вихревого электрического поля (т. е. чтобы они пересекали возможные линии вихревых токов).

Нагрев вихревыми токами массивных проводников используется в индукционных печах для плавки металлов и изготовления сплавов.

ЭДС индукции в движущихся проводниках

ЭДС индукции в проводниках, движущихся в постоянном магнитном поле, соответствует второму типу электромагнитной индукции, обусловленному не переменным внешним магнитным полем, а действием сил Лоренца на свободные заряды проводника.

ЭДС индукции, возникающая на концах проводника длиной $l$, движущегося с постоянной скоростью $υ↖{→}$ под некоторым углом $α$ к вектору индукции $В↖{→}$ однородного магнитного поля, равна:

$ε_i={A}/{|q|}={F_{L}l}/{|q|}={|q|υBlsinα}/{|q|}=υBlsinα$

где $А$ — работа силы Лоренца по перемещению заряда $q$ на пути $l, F_L$ — сила Лоренца, действующая на движущийся заряд.

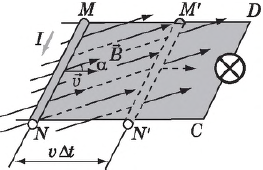
Если такой проводник входит в состав замкнутой цепи, остальные части которой неподвижны, то в цепи возникает электрический ток. Сила тока равна:

$I={ε_i}/{R+r}={υBlsinα}/{R+r}$

где $R$ — сопротивление нагрузки (лампочки); $r$ — сопротивление проводника, играющего роль внутреннего сопротивления источника тока (сопротивлением соединяющих проводников пренебрегаем).

С другой стороны, ту же ЭДС индукции можно получить, используя основной закон электромагнитной индукции $ε_i=-{∆Ф}/{∆t}$ и формулу $Ф=B_{n}S$:

$ε_i=-{∆Ф}/{∆t}={BSsinα}/{∆t}$

В данном случае изменение потока осуществляется не за счет изменения индукции поля, а за счет изменения площади контура, равного $∆S=-lυ∆t$. В результате получим:

$ε_i=υBlsinα$

Правило Ленца

Правило Ленца (закон Ленца) было установлено Э. X. Ленцем в 1834 г. Оно уточняет закон электромагнитной индукции, открытый в 1831 г. М. Фарадеем. Правило Ленца определяет направление индукционного тока в замкнутом контуре при его движении во внешнем магнитном поле.

Направление индукционного тока всегда таково, что испытываемые им со стороны магнитного поля силы противодействуют движению контура, а создаваемый этим током магнитный поток $Ф_1$ стремится компенсировать изменения внешнего магнитного потока $Ф_e$.

Закон Ленца является выражением закона сохранения энергии для электромагнитных явлений. Действительно, при движении замкнутого контура в магнитном поле за счет внешних сил необходимо выполнить некоторую работу против сил, возникающих в результате взаимодействия индуцированного тока с магнитным полем и направленных в сторону, противоположную движению.

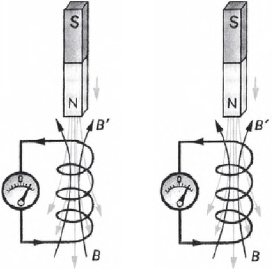
Правило Ленца иллюстрируют рисунок. Если постоянный магнит вдвигать в катушку, замкнутую на гальванометр, индукционный ток в катушке будет иметь такое направление, которое создаст магнитное поле с вектором $В'$, направленным противоположно вектору индукции поля магнита $В$, т. е. будет выталкивать магнит из катушки или препятствовать его движению. При вытягивании магнита из катушки, наоборот, поле, создаваемое индукционным током, будет притягивать катушку, т. е опять препятствовать его движению.

Для применения правила Ленца с целью определения направления индукционного тока $I_е$ в контуре необходимо следовать таким рекомендациям.

1. Установить направление линий магнитной индукции $В↖{→}$ внешнего магнитного поля.
2. Выяснить, увеличивается ли поток магнитной индукции этого поля через поверхность, ограниченную контуром ($∆Ф > 0$), или уменьшается ($∆Ф < 0$).
3. Установить направление линий магнитной индукции $В'↖{→}$ магнитного поля индукционного тока $I_i$. Эти линии должны быть направлены, согласно правилу Ленца, противоположно линиям $В↖{→}$, если $∆Ф > 0$,и иметь одинаковое с ними направление, если $∆Ф < 0$.
4. Зная направление линий магнитной индукции $В'↖{→}$, определить направление индукционного тока $I_i$, пользуясь правилом буравчика.