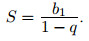Прогрессии
1. Если an есть n-й член, d— разность и Sn — сумма n первых членов арифметической прогрессии, то
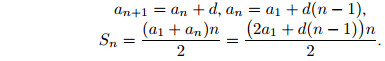
Арифметическая прогрессия возрастает, если d > 0, и убывает, если
d < 0.
2*. Если ak, al, am, an — члены арифметической прогрессии с такими номерами,
что k + l = m + n, то ak + al = am+an.
3. Каждый член арифметической прогрессии, отличный от первого и последнего, равен среднему арифметическому соседних с ним членов:
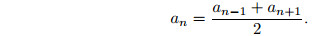
Геометрическая прогрессия
1. Если bn есть n-й член, q — знаменатель и Sn — сумма n первых членов геометрической прогрессии, то
bn+1= bnq, b1 ≠ 0, q ≠ 0; bn = b1qn-1,
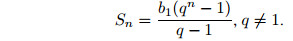
2*. Если bk, bl, bm, bn — члены геометрической прогрессии с такими номерами,
что k + l = m + n, то bk + bl = bm+bn.
3. Квадрат каждого члена геометрической прогрессии, отличного от первого и последнего, равен произведению соседних с ним членов:

Бесконечно убывающая геометрическая прогрессия
Если S есть сумма бесконечно убывающей геометрической прогрессии (|q| < 1), то