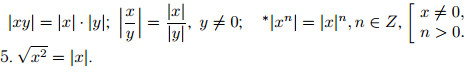Метод рационализации
Рациональным называется всякое неравенство, сводящееся к неравенству вида
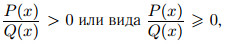
где P(x), Q(x) — некоторые многочлены.
| Поскольку | 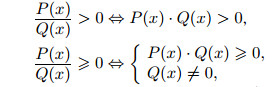 |
Пример. Решите неравенство
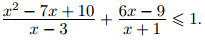
Решение.
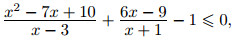
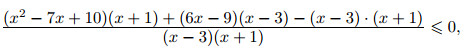
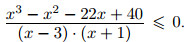
Числитель последней дроби разложим на множители. Подбором находим, что x = 2 является корнем многочлена
x3 − x2 − 22x + 40; разделив данный многочлен (уголком или по схеме Горнера) на x − 2, получаем
x3 − x2 − 22 x + 40 = (x − 2)·(x2 + x − 20) = (x − 2)·(x − 4)·(x + 5). Значит, исходное неравенство равносильно системе
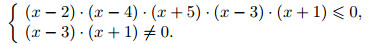
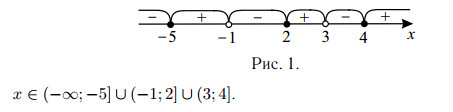
Решая первое неравенство этой системы методом интервалов (см. рис. 1) и выкалывая точки $x = −1, x = 3$, получаем ответ
Определение модуля числа

2. Геометрически |x| есть расстояние от точки x числовой оси до начала отсчёта — точки O.
3. |x − a| есть расстояние между точками x и a числовой оси.
4. Модуль произведения, частного и степени.