Закон Амантона-Кулона. Сила трения

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.

Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

В аналитическом виде закон Кулона имеет вид:

$F=k{|q_1|·|q_2|}/{r^2}$

где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.

То есть $1$ Кл$= 1А·с$.

Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).

Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:

$k=9·10^9H·м^2$/$Кл^2$

Часто его записывают в виде $k={1}/{4πε_0}$, где $ε_0=8.85×10^{-12}Кл^2$/$H·м^2$ - электрическая постоянная.

Сила трения

Взаимодействие, возникающее в месте соприкосновения тел и препятствующее их относительному движению, называют трением, а характеризующую это взаимодействие силу — силой трения.

Силы трения, как и силы упругости, имеют электромагнитную природу. Трение между двумя твердыми телами называют сухим трением.

Различают три вида трения: трение покоя, трение скольжения и трение качения.

1. Трение покоя — трение, возникающее при отсутствии относительного перемещения соприкасающихся тел.

Трение покоя удерживает грузы, находящиеся на движущейся ленте транспортера, от соскальзывания, препятствует развязыванию шнурков, удерживает гвозди, вбитые в доску, и т. д.

Сила трения покоя — это сила, препятствующая возникновению движения одного тела относительно другого. Направлена сила трения покоя всегда против силы, приложенной извне параллельно поверхности соприкосновения и стремящейся сдвинуть с места предмет, т. е. против предполагающегося движения. Измерить силу трения покоя можно с помощью груза, перекинутого через блок и связанного с телом через динамометр.

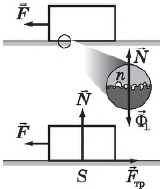
Сила трения покоя растет вместе с силой, стремящейся сдвинуть тело с места. Но для любых двух соприкасающихся тел она имеет некоторое максимальное значение $(F_{тр.п.}){max}$, больше которого она быть не может. Например, для деревянного бруска, находящегося на деревянной доске, максимальная сила трения покоя составляет $0.6$ от его веса. Максимальная сила трения покоя пропорциональна силе нормального давления, равного по модулю силе реакции опоры $N$:

$(F{тр.п.}){max}=μ{п}N$,

где $μ_{п}$ — коэффициент трения покоя.

Максимальная сила трения покоя не зависит от площади соприкосновения поверхностей. Она зависит от качества обработки соприкасающихся поверхностей и от материалов тел.

2. Трение скольжения. Приложив к телу силу, превышающую максимальную силу трения покоя, мы сдвинем тело с места, и оно начнет двигаться. Трение покоя при этом сменится трением скольжения.

Сила трения скольжения всегда направлена в сторону, противоположную относительной скорости соприкасающихся тел.

Как и максимальная сила трения покоя, сила трения скольжения пропорциональна силе нормального давления и, следовательно, силе реакции опоры:

$F_{тр}=μN$,

где $μ$ — коэффициент трения скольжения (при небольших скоростях $μ < μ_{п}$), зависящий от свойств соприкасающихся поверхностей.

Сила трения скольжения зависит также довольно сложным образом от относительной скорости соприкасающихся тел. При небольших относительных скоростях сила трения скольжения меньше силы трения покоя, и лишь при увеличении скорости $F_{тр} > (F_{тр.п.}){max}$.

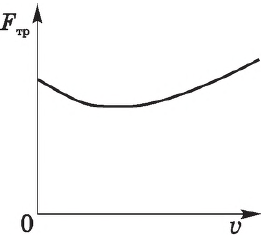
При небольших скоростях приближенно их можно считать равными:

$F{тр}=(F_{тр.п.}){max}=μN$

Причины возникновения силы трения

1. Шероховатость поверхностей соприкасающихся тел. Даже те поверхности, которые выглядят гладкими, на самом деле всегда имеют микроскопические неровности (выступы, впадины). При скольжении одного тела по поверхности другого эти неровности зацепляются друг за друга и всегда мешают движению.
2. Межмолекулярное притяжение, действующее в местах контакта трущихся тел. Межмолекулярное притяжение проявляется в тех случаях, когда поверхности соприкасающихся тел хорошо отполированы. Так, например, при относительном скольжении двух металлов с очень чистыми и ровными поверхностями, обработанными в вакууме с помощью специальной технологии, сила трения оказывается намного больше, чем при перемещении неровного бруска дерева по земле. В некоторых случаях эти металлы даже «схватываются» друг с другом, и дальнейшее скольжение невозможно.
3. Трение качения. Если тело не скользит по поверхности другого тела, а, подобно колесу или цилиндру, катится, то возникающее в месте их контакта трение называют трением качения. Катящееся колесо все время вдавливается в полотно дороги, и потому перед ним все время оказывается небольшой бугорок, который необходимо преодолеть. Именно этим и обусловлено трение качения. При этом чем дорога тверже, тем трение качения меньше.

Как и в предыдущих случаях, сила трения качения пропорциональна силе реакции опоры:

$F{тр.кач.}=μ_{кач.}N$,

где $μ_{кач.}$ — коэффициент трения качения.

Благодаря тому, что $μ_{кач.} << μ$, при одинаковых нагрузках сила трения качения значительно меньше силы трения скольжения. Это было замечено еще в древности. Поэтому для перемещения тяжелых грузов наши предки подкладывали под них катки или бревна. По этой же причине люди стали использовать в транспорте колеса.

Разница в силах трения скольжения и качения объясняется тем, что при скольжении участки тела смещаются вдоль поверхности соприкосновения, и вместо разорванных межмолекулярных связей постоянно образуются новые. Когда колесо катится без проскальзывания по поверхности, молекулярные связи разрываются при подъеме участков колеса быстрее, чем при скольжении, и поэтому сила трения качения значительно меньше силы трения скольжения.

Сила сопротивления твердого тела, движущегося в жидкости и газе

На твердое тело, движущееся в жидкости или газе, действует сила сопротивления среды. Эта сила направлена против скорости тела относительно среды и тормозит движение.

В отличие от силы трения сила сопротивления среды появляется только во время движения тела в этой среде. Ничего подобного силе трения покоя здесь нет. Наоборот, всем известно, насколько легче сдвинуть с места предмет в воде, чем на твердой поверхности.

Модуль силы сопротивления среды $F_с$ зависит от размеров, формы и состояния поверхности тела, свойств жидкости или газа, в котором тело движется, и от относительной скорости движения тела и среды. Примерный характер зависимости $F_с$ от скорости $υ$ приведен на рисунке.

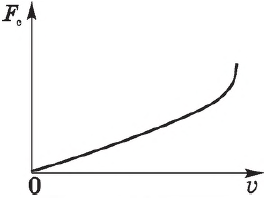
При малых скоростях движения тела относительно среды можно считать

$F_c=k_1υ$,

где $k_1$ — коэффициент, зависящий от размеров, формы, состояния поверхности тела и вязкости среды.

При больших скоростях относительного движения сила сопротивления пропорциональна квадрату скорости:

$F_c=k_2υ^2$,

где $k_2$ — коэффициент сопротивления, отличный от $k_1$.