Механическая работа, мощность

Работа силы

Термин «работа» был введен в физику в 1826 г. французским ученым Ж. Понселе. Если в обыденной жизни работой называют лишь труд человека, то в физике и, в частности, в механике принято считать, что работу совершает сила. Физическую величину работы обычно обозначают буквой $А$.

Работа силы — это мера действия силы, зависящая от ее модуля и направления, а также от перемещения точки приложения силы. Для постоянной силы и прямолинейного перемещения работа определяется равенством:

$A=F|∆r↖{→}|cosα$

где $F$ — сила, действующая на тело, $∆r↖{→}$ — перемещение, $α$ — угол между силой и перемещением.

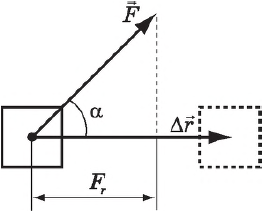
Работа силы равна произведению модулей силы и перемещения и косинуса угла между ними, т. е. скалярному произведению векторов $F↖{→}$ и $∆r↖{→}$.

Работа — величина скалярная. Если $α < 90°$, то $А > 0$, а если $90° < α < 180°$, то $A < 0$; если же $α = 90°$, то $А = 0$. Так, сила тяжести не совершает работу при перемещении тела по горизонтальной плоскости. Также при движении спутника по круговой орбите сила тяготения не совершает работу.

При действии на тело нескольких сил полная работа (сумма работ всех сил) равна работе результирующей силы.

Единицей работы в СИ является джоуль ($1$ Дж). $1$ Дж — это работа, которую совершает сила в $1$ Н на пути в $1$ м в направлении действия этой силы. Эта единица названа в честь английского ученого Дж. Джоуля (1818-1889): $1$ Дж = $1$ Н $·$ м. Часто применяются также килоджоули и миллиджоули: $1$ кДж $= 1 000$ Дж, $1$ мДж $= 0.001$ Дж.

Работа силы тяжести

Рассмотрим тело, скользящее по наклонной плоскости с углом наклона $α$ и высотой $Н$.

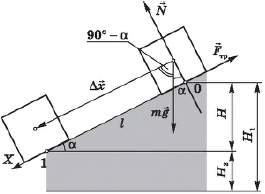
Выразим $∆x$ через $H$ и $α$:

$∆x={H}/{sinα}$

Учитывая, что сила тяжести $F_т=mg$ составляет угол ($90° - α$) с направлением перемещения, используя формулу $∆x={H}/{sin}α$, получим выражение для работы силы тяжести $A_g$:

$A_g=mg·cos(90°-α)·{H}/{sinα}=mgH$

Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.

Отсюда следует, что:

1. работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
2. при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).

Работа сил реакции, равна нулю, поскольку сила реакции ($N$) направлена перпендикулярно перемещению $∆x$.

Работа силы трения

Сила трения направлена противоположно перемещению $∆x$ и составляет с ним угол $180°$, поэтому работа силы трения отрицательна:

$A_{тр}=F_{тр}∆x·cos180°=-F_{тр}·∆x$

Так как $F_{тр}=μN, N=mg·cosα, ∆x=l={H}/{sinα},$ то

$A_{тр}=μmgHctgα$

Работа силы упругости

Пусть на нерастянутую пружину длиной $l_0$ действует внешняя сила $F↖{→}$, растягивая ее на $∆l_0=x_0$. В положении $x=x_0F_{упр}=kx_0$. После прекращения действия силы $F↖{→}$ в точке $х_0$ пружина под действием силы $F_{упр}$ сжимается.

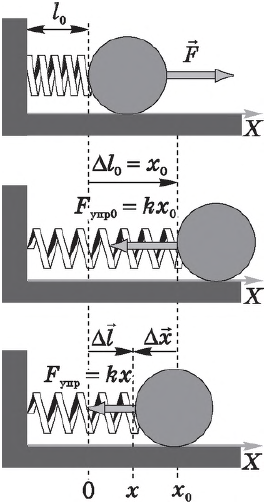
Определим работу силы упругости при изменении координаты правого конца пружины от $х_0$ до $х$. Поскольку сила упругости на этом участке изменяется линейно, в законе Гука можно использовать ее среднее значение на этом участке:

$F_{упр.ср.}={kx_0+kx}/{2}={k}/{2}(x_0+x)$

Тогда работа (с учетом того, что направления ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$ совпадают) равна:

$A_{упр}={k}/{2}(x_0+x)(x_0-x)={kx_0^2}/{2}-{kx^2}/{2}$

Можно показать, что вид последней формулы не зависит от угла между ${F_{упр.ср.}}↖{→}$ и ${∆x}↖{→}$. Работа сил упругости зависит лишь от деформаций пружины в начальном и конечном состояниях.

Таким образом, сила упругости, подобно силе тяжести, является консервативной силой.

Мощность силы

Мощность — физическая величина, измеряемая отношением работы к промежутку времени, в течение которого она произведена.

Другими словами, мощность показывает, какая работа совершается за единицу времени (в СИ — за $1$ с).

Мощность определяется формулой:

$N={A}/{∆t}$

где $N$ — мощность, $А$ — работа, совершенная за время $∆t$.

Подставив в формулу $N={A}/{∆t}$ вместо работы $A$ ее выражение $A=F|{∆r}↖{→}|cosα$, получим:

$N={F|{∆r}↖{→}|cosα}/{∆t}=Fυcosα$

Мощность равна произведению модулей векторов силы и скорости на косинус угла между этими векторами.

Мощность в системе СИ измеряется в ваттах (Вт). Один ватт ($1$ Вт) — это такая мощность, при которой за $1$ с совершается работа $1$ Дж: $1$ Вт $= 1$ Дж/с.

Эта единица названа в часть английского изобретателя Дж. Ватта (Уатта), построившего первую паровую машину. Сам Дж. Ватт (1736-1819) пользовался другой единицей мощности — лошадиной силой (л. с.), которую он ввел для того, чтобы можно было сравнивать работоспособности паровой машины и лошади: $1$ л.с. $= 735.5$ Вт.

В технике часто применяются более крупные единицы мощности — киловатт и мегаватт: $1$ кВт $= 1000$ Вт, $1$ МВт $= 1000000$ Вт.