Текстовые задачи (2 часть)

Задачи на движение

 Задания B14 — текстовые задачи на движение, сравнительную скорость выполнения определённого задания или на совместную работу. Чтобы решать задачи на движение, достаточно знать формулу пути при равномерном движении (то есть движении с постоянной скоростью) и её следствия для вычисления времени или скорости:

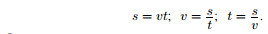
 Здесь s — путь, t — время, v — скорость.
 В задачах на движение по течению или против течения реки нужно к тому же понимать, что при движении по течению (иногда говорят «вниз по течению») скорость реки прибавляется, а против течения («вверх по течению») — отнимается от собственной скорости транспорта (лодки, катера, теплохода). Скорость плота (бревна) совпадает со скоростью течения реки. На озере вода считается стоячей (скорость течения нулевая).
 Чтобы составить уравнение, данные из условия и их следствия лучше всего занести в таблицу.

	Расстояние (км)	Скорость (км/ч)	Время (ч)
A	s1	v1	t1
B	s2	v2	t2

 Конкретное содержание и последовательность заполнения клеток таблицы зависит от специфики задания. Рассмотрим типичные из них.

 Задачи с решениями
 Из одного города в другой выехали одновременно двое байкеров. Первый проехал весь путь с постоянной скоростью. Второй проехал первую половину пути со скоростью 80 км/ч, а вторую — со скоростью на 24 км/ч больше, чем скорость первого байкера. Определите скорость первого байкера, если в другой город они приехали одновременно. Ответ дайте в км/ч
 Решение.
 Пусть скорость первого байкера равна x км/ч. Обозначим через s половину расстояния между городами. Первый байкер проехал 2s км за


 Так как по условию время движения первого байкера равно времени движения второго байкера, то имеет место следующее уравнение:

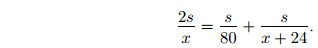
 Разделив обе части последнего равенства на s, получим дробнорациональное уравнение, решаемое умножением левой и правой частей на общий знаменатель. Решают его последующим сокращением и получением целого уравнения (то есть уравнения без деления на переменную). Затем, после нахождения корней этого уравнения, их проверяют на соответствие реальному смыслу задачи (и на неравенство нулю общего знаменателя).
 Решим наше уравнение.

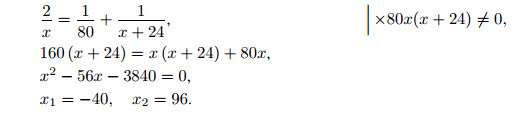
 Первый корень явно не подходит по смыслу задачи, потому что скорость должна быть положительна. Следовательно, скорость первого байкера 96 км/ч.
 Ответ: 96
 Примечание. Математическую модель задачи можно упростить, приняв длину половины пути за 1, тогда весь путь равен 2. Так можно делать, когда в задаче не задано численно ни одного участка пути.

 Рыбнадзорный катер патрулирует участок реки длиной 180 км. Против течения реки он проплывает этот участок за время, на 1 час большее, чем по течению реки. Определите скорость катера в стоячей воде (собственная скорость), если скорость течения реки равна 1 км/ч. Ответ дайте в км/ч.
 Решение.
 Обозначим скорость катера в стоячей воде через x км/ч. Тогда скорость катера по течению равна x + 1 км/ч, а против течения — x − 1 км/ч. Заполним таблицу по условию задачи.

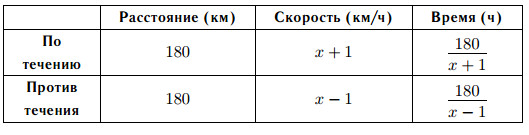
 Составим и решим уравнение.

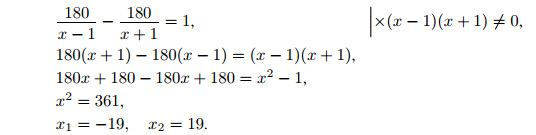
 Отрицательный корень не подходит по смыслу задачи. Итак, скорость катера в стоячей воде равна 19 км/ч.
 Ответ: 19.
 Примечание. Среди задач данного раздела встречаются условия задержек в пути. Длительность таких пауз приходится дополнительно включать в уравнения. Не забывайте при этом переводить всё в одинаковые единицы.

Задачи на совместную работу

 Скорость присутствует не только в задачах на движение, но и в задачах на сравнительную быстроту выполнения какого-либо задания. Поэтому и математические модели соответствующих задач строятся совершенно аналогично.
 Задачи с решениями
 10. На сбор 2400 бонусов первый геймер тратит времени на 20 минут меньше, чем второй. Сколько бонусов в минуту собирает второй геймер, если первый собирает в минуту на 20 бонусов больше?
 Решение.
 Пусть второй геймер собирает х бонусов в минуту, тогда первый собирает x + 20 бонусов в минуту. Табличная версия задачи имеет следующий вид:

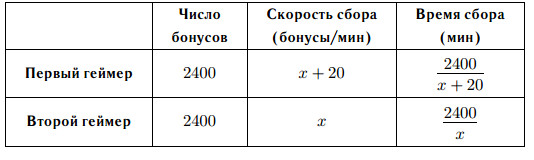
 Составим и решим уравнение.

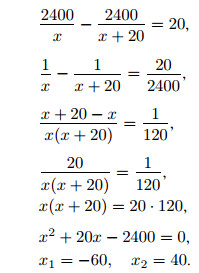
 Отрицательный корень не подходит по смыслу задачи. Итак, второй геймер собирает 40 бонусов в минуту.
 Ответ: 40