Геометрическая задача на вычисление повышенной сложности (2 часть)
Пусть an — сторона правильного n-угольника, а rn и Rn — радиусы вписанной и описанной окружностей. Тогда
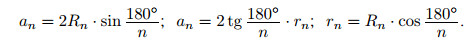
Формула Герона для четырёхугольника, около которого можно описать окружность:
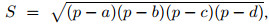 |
где a, b, c, d — стороны этого четырёхугольника, p — полупериметр, а S — площадь. |
Окружностью называется геометрическое место точек плоскости, равноудалённых от данной точки, называемой центром окружности.
Основные свойства окружности
1. Диаметр, перпендикулярный хорде, делит хорду и стягиваемые ею дуги пополам.
2. Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
3. Серединный перпендикуляр к хорде проходит через центр окружности.
4. Равные хорды удалены от центра окружности на равные расстояния.
5. Хорды окружности, удалённые от центра на равные расстояния, равны.
6. Окружность симметрична относительно любого своего диаметра.
7. Дуги окружности, заключённые между параллельными хордами, равны.
8. Из двух хорд больше та, которая менее удалена от центра.
9. Диаметр есть наибольшая хорда окружности.
Замечательные свойства окружности
1. Геометрическое место точек M, из которых отрезок AB виден под прямым углом (∠AMB = 90°), есть окружность с диаметром AB без точек A и B
2. Геометрическое место точек M, из которых отрезок AB виден под острым углом (∠AMB < 90°), есть внешность круга с диаметром AB без точек прямой AB.
3. Геометрическое место точек M, из которых отрезок AB виден под тупым углом (∠AMB > 90°), есть внутренность круга с диаметром AB без точек отрезка AB
4. Геометрическое место точек, из которых данный отрезок виден под данным углом, есть две дуги равных окружностей (без концов этих дуг).
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
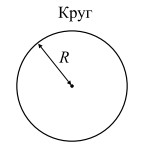 |
R — радиус; l — длина окружности |
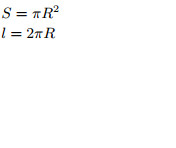 |
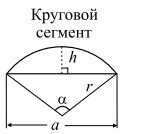 |
r — внутренний радиус; R — наружный радиус; d — внутренний диаметр; D — наружный диаметр; 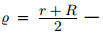 средний радиус; δ = R − r — ширина кольца; α — центральный угол части кольца (в градусах). |
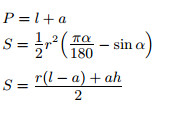 |
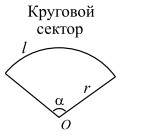 |
r — радиус; α — центральный угол (в градусах); 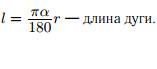
|
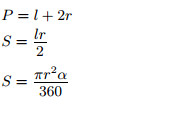 |
Площади круга и сектора
Площадь круга равна произведению числа π на квадрат радиуса:S = πR2.
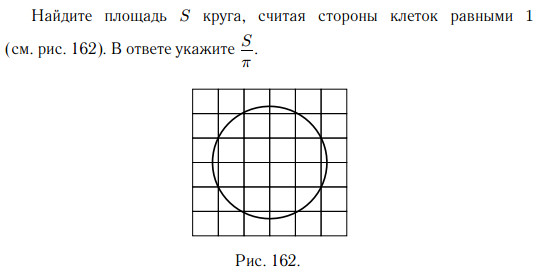
Решение.
Площадь круга равна произведению числа π на квадрат радиуса. Найдём радиус. Из центра O проведём радиус OA. В треугольнике OAB сторона OA — гипотенуза, катеты равны 1 и 2 (см. рис. 163)
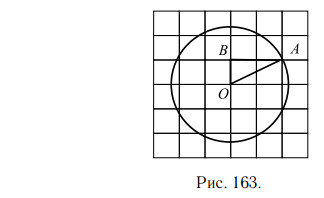
Найдём гипотенузу по теореме Пифагора.

Ответ: 5
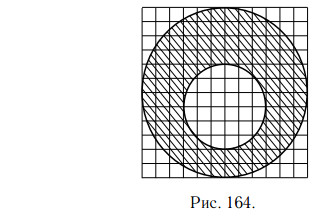
На клетчатой бумаге нарисовано два круга (см. рис. 164). Площадь внутреннего круга равна 3. Найдите площадь заштрихованной фигуры.
Решение.
Радиус R внутреннего круга — 3 клетки, его площадь равна πR2 = 3. Радиус внешнего круга — 6 клеток, то есть 2R, поэтому его площадь равна π · (2R)2 = 3 · 4 = 12. Площадь заштрихованной фигуры равна разности 12 − 3 = 9.
Ответ: 9

Признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
2. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то треугольники равны.
3. Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то треугольники равны.
Признаки равенства прямоугольных треугольников
1. По двум катетам.
2. По катету и гипотенузе.
3. По гипотенузе и острому углу
4. По катету и острому углу
Теорема о сумме углов треугольника и следствия из неё
1. Сумма внутренних углов треугольника равна 180°.
2. Внешний угол треугольника равен сумме двух внутренних не смежных с ним углов.
3. Сумма внутренних углов выпуклого n-угольника равна 180°(n − 2).
4. Сумма внешних углов n-угольника равна 360°
5. Углы со взаимно перпендикулярными сторонами равны, если они оба острые или оба тупые.
6. Угол между биссектрисами смежных углов равен 90°.
7. Биссектрисы внутренних односторонних углов при параллельных прямых и секущей перпендикулярны.
Основные свойства и признаки равнобедренного треугольника
1. Углы при основании равнобедренного треугольника равны.
2. Если два угла треугольника равны, то он равнобедренный.
3. В равнобедренном треугольнике медиана, биссектриса и высота, проведённые к основанию, совпадают.
4. Если в треугольнике совпадает любая пара отрезков из тройки: медиана, биссектриса, высота, — то он является равнобедренным.
Неравенство треугольника и следствия из него
1. Сумма двух сторон треугольника больше его третьей стороны
2. Сумма звеньев ломаной больше отрезка, соединяющего начало первого звена с концом последнего.
3. Против большего угла треугольника лежит бOльшая сторона.
4. Против большей стороны треугольника лежит больший угол.
5. Гипотенуза прямоугольного треугольника больше катета
6. Если из одной точки проведены к прямой перпендикуляр и наклонные, то
1) перпендикуляр короче наклонных;
2) большей наклонной соответствует большая ´ проекция и наоборот
Средняя линия треугольника. Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.
Теорема о средней линии треугольника. Средняя линия треугольника параллельна стороне треугольника и равна её половине.
Теоремы о медианах треугольника
1. Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2 : 1, считая от вершины.
2. Если медиана треугольника равна половине стороны, к которой она проведена, то треугольник прямоугольный
3. Медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы
Свойство серединных перпендикуляров к сторонам треугольника. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке, которая является центром окружности, описанной около треугольника
Теорема о высотах треугольника. Прямые, содержащие высоты треугольника, пересекаются в одной точке.
Теорема о биссектрисах треугольника. Биссектрисы треугольника пересекаются в одной точке, которая является центром окружности, вписанной в треугольник.
Свойство биссектрисы треугольника. Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам
Признаки подобия треугольников
1. Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
2. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого, а углы, заключенные между этими сторонами, равны, то треугольники подобны.
3. Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого, то треугольники подобны.
Площади подобных треугольников
1. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
2. Если два треугольника имеют равные углы, то их площади относятся как произведения сторон, заключающих эти углы.
В прямоугольном треугольнике
1. Катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего или на косинус прилежащего к этому катету острого угла.
2. Катет прямоугольного треугольника равен другому катету, умноженному на тангенс противолежащего или на котангенс прилежащего к этому катету острого угла.
3. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
4. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, противолежащий этому катету, равен 30°.
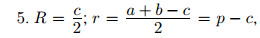
где a, b — катеты, а c — гипотенуза прямоугольного треугольника; r и R — радиусы вписанной и описанной окружностей соответственно
Теорема Пифагора и теорема, обратная теореме Пифагора
1. Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
2. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник — прямоугольный
Средние пропорциональные в прямоугольном треугольнике
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу, а каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу
Метрические соотношения в треугольнике
1. Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
2. Следствие из теоремы косинусов. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
3. Формула для медианы треугольника. Если m — медиана треугольника, проведённая к стороне c, то
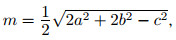 где a и b — остальные стороны треугольника.
где a и b — остальные стороны треугольника.4. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.
5. Обобщённая теорема синусов. Отношение стороны треугольника к синусу противолежащего угла равно диаметру окружности, описанной около треугольника.
Формулы площади треугольника
1. Площадь треугольника равна половине произведения основания на высоту.
2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
3. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
4. Площадь треугольника равна произведению трёх его сторон, делённому на учетверённый радиус описанной окружности.
5. Формула Герона:
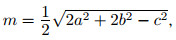
где p — полупериметр; a, b, c — стороны треугольника.
Элементы равностороннего треугольника
Пусть h, S, r, R — высота, площадь, радиусы вписанной и описанной окружностей равностороннего треугольника со стороной a. Тогда
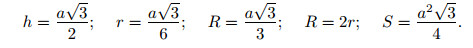
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
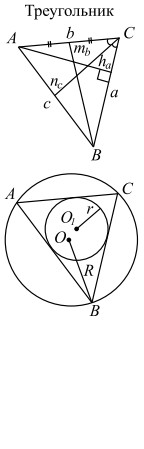 |
a, b, c — стороны; A, B, C — противолежащие им углы; ha, hb, hc — высоты, проведённые к соответствующим сторонам; na, nb, nc — биссектрисы, проведённые к соответствующим сторонам; ba и bc — отрезки, на которые делится биссектрисой сторона b; ma, mb, mc — медианы, проведённые к соответствующим сторонам; 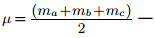 полусумма медиан; R — радиус описанной окружности; r — радиус вписанной окружности |
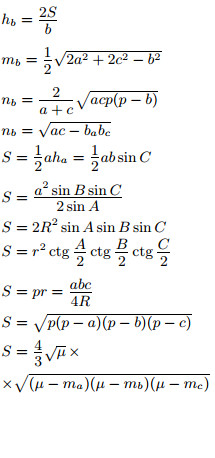 |
Прямоугольный треугольник
Немного полезной информации
В этой главе мы рассмотрим простые виды задач по геометрии, а именно задачи, в которых нужно найти площади плоских фигур, нарисованных на клетчатой бумаге или расположенных на координатной плоскости.Для решения таких задач требуется знать не очень много формул, поэтому их решение доступно практически каждому. Давайте вспомним эти формулы и разберём примеры их применения.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы (c) равен сумме квадратов катетов (a и b):
c2 = a2 + b2
Площадь прямоугольного треугольника равна половине произведения его катетов:
S =ab/2.
Напомним, что у прямоугольного треугольника есть прямой угол, равный 90°. Сторона напротив прямого угла (самая длинная) называется гипотенузой, две прилежащие к прямому углу стороны называют катетами.
На рисунке 147 приведены чертежи некоторых прямоугольных треугольников, у которых показаны катеты a и b.
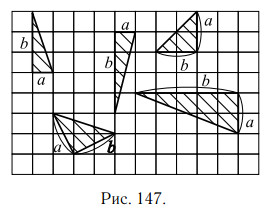
Задачи с решениями
1. На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 148). Найдите его площадь в квадратных сантиметрах.
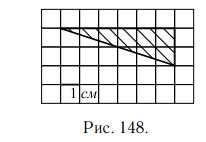
Решение.
Площадь прямоугольного треугольника равна половине произведения его катетов. В данном треугольнике катеты равны 2 см и 6 см (посчитаем по клеточкам), поэтому площадь
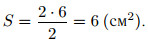
Ответ: 6
Площадь треугольника
Немного полезной информации
Площадь произвольного треугольника равна половине произведения длины его стороны (a) на высоту (h), проведённую к этой стороне: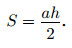
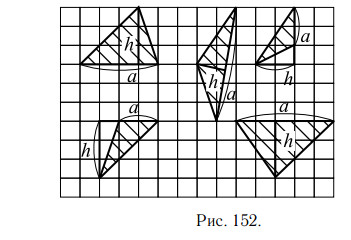
На рисунке 152 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон a и высота, проведённая к этой стороне h.
Как правило, удобно брать ту сторону, которая проходит по линиям клетчатой бумаги (или же проходит параллельно осям координат).
Задачи с решениями
На клетчатой бумаге с клетками размером 1 см × 1 см изображён треугольник (см. рис. 153). Найдите его площадь в квадратных сантиметрах.
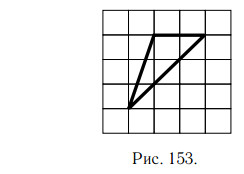
Решение.
1-й способ.
Площадь произвольного треугольника равна половине произведения длины его стороны (a) на высоту (h), проведённую к этой стороне. Проведём высоту h. Треугольник тупоугольный, поэтому высота проводится вне треугольника.
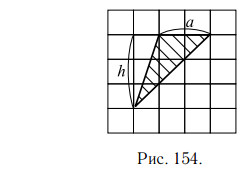
На рисунке 154 сторона a = 2 см, высота h = 3 см
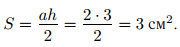
Ответ: 3.
Заметим, что так как клетки имеют размер 1 см × 1 см, то площадь в квадратных сантиметрах получится, если мы будем по рисунку считать размер отрезков в клетках. Поэтому единицы длины в этих задачах можно и не писать.
2-й способ.
Достроим треугольник BCM до прямоугольного треугольника MCA (см. рис. 155).
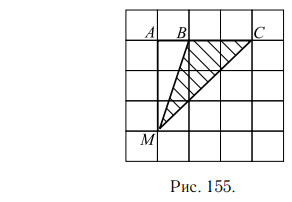
Тогда искомую площадь треугольника BCM можно найти как разность площадей двух прямоугольных треугольников MAC и MAB.
Катеты первого из них равны 3 см и 3 см, катеты второго — 3 см и 1 см. Площадь прямоугольного треугольника равна половине произведения его катетов, следовательно,
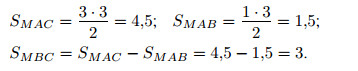
Ответ: 3.
Четырёхугольник
Параллелограмм.
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.Свойства и признаки параллелограмма
1. Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
5. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Свойство середин сторон четырёхугольника. Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольник
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.
Формулы площади четырёхугольника
1. Площадь параллелограмма равна произведению основания на высоту
2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
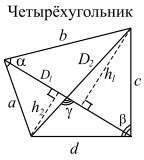 |
a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h1, h2 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. |
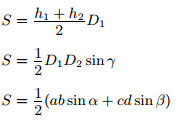 |
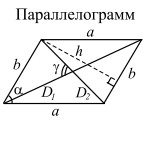 |
a, b — стороны; h — расстояние между сторонами b; α — угол параллелограмма; D1, D2 — диагонали; γ — угол между диагоналями |
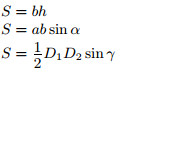 |
Площадь четырёхугольника
Площадь прямоугольника равна произведению его смежных сторон:S = ab.
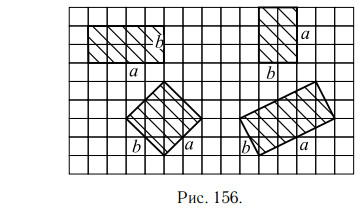
На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b
Ромб
Квадрат. Квадратом называется прямоугольник, все стороны которого равны.Свойства и признаки ромба
1. Диагонали ромба перпендикулярны.
2. Диагонали ромба делят его углы пополам
3. Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
4. Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
Площадь ромба равна половине произведения его диагоналей
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
 |
a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h1, h2 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. |
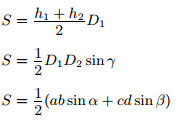 |
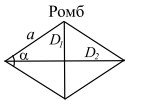 |
a — сторона; α — угол ромба; D1, D2 — диагонали. |
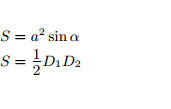 |
Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны. Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).1. Теорема о средней линии трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции. Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция. Трапеция называется равнобедренной, если её боковые стороны равны.
Свойства и признаки равнобедренной трапеции
1. Углы при основании равнобедренной трапеции равны.
2. Диагонали равнобедренной трапеции равны
3. Если углы при основании трапеции равны, то она равнобедренная.
4. Если диагонали трапеции равны, то она равнобедренная
5. Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали — полусумме оснований.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
 |
a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h1, h2 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. |
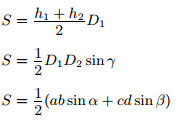 |
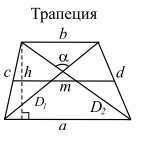 |
a, b — основания; c, d — боковые стороны; D1, D2 — диагонали; α — угол между диагоналями; m — средняя линия; h — высота |
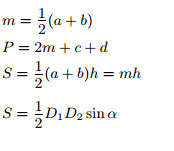 |
Площадь трапеции равна половине произведения суммы оснований (a + b) на высоту (h):

На рисунке 168 приведены чертежи некоторых трапеций, у каждой из которых показаны основания a и b и высота h.
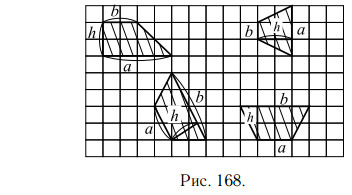
Площадь четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.
| Чертежи | Обозначения | Формулы |
 |
a, b, c, d — стороны; D1, D2 — диагонали; γ — угол между диагоналями; h1, h2 — длины перпендикуляров, опущенных на диагональ D1; α, β — два противолежащих угла четырёхугольника. |
 |
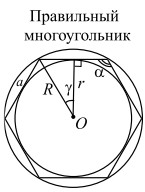 |
n — число сторон; a — сторона; R — радиус описанной окружности; r — радиус вписанной окружности; α = 180° − 2γ — угол многоугольника 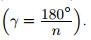
|
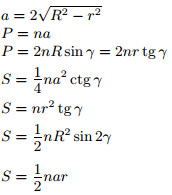 |





