Анализ моделей. Соотнесение таблицы и графа
Теория к заданию 1 из ЕГЭ по информатике
Представление и считывание данных в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы)
Многообразие объектов предполагает использование огромного количества инструментов для реализации и описания этих моделей. Для исследования большинства объектов не обязательно создавать материальные модели. Если ясно представлять цель исследования, то часто достаточно иметь нужную информацию и представить ее в оптимальной форме. В этом случае речь идет о создании информационной модели. Информационные модели — это абстрактные модели, поскольку, как известно, информация — это нематериальная категория.
Информационная модель — это целенаправленно отобранная информация об объекте, представленная в некоторой форме.
Простейшими примерами информационных моделей являются различные загадки, в которых описываются свойства, по которым нужно угадать название объекта («Летом серый, зимой белый»; «Зимой и летом одним цветом»). К информационным моделям можно отнести тексты справочных изданий, энциклопедий.
Формы представления информационных моделей могут быть различными. Наиболее известны следующие формы:
- в виде сигналов;
- устная, словесная;
- символьная (числа, текст, символы);
- табличная;
- схемы, карты;
- графики.
Один и тот же объект, в зависимости от поставленной цели, можно представить несколькими информационными моделями, отличающимися набором параметров и способом их представления. Рассмотрим примеры анализа информации для модели, представленной в табличной форме.
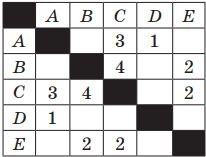
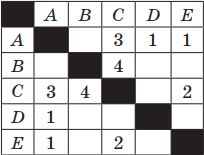
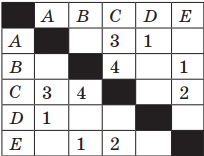
Пример 1. Таблица стоимости перевозок между станциями A, B, C, D, E построена следующим образом: числа, стоящие в ячейках на пересечении строк и столбцов, означают стоимость проезда между соответствующими соседними станциями. Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями. Если на пересечении строки и столбца пусто, то станции не являются соседними. Выбрать таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6».
Решение. Прежде всего, нужно отметить, что данные в таблицах симметричны относительно главной диагонали, т. е. проезд из А в В стоит столько же, сколько и из В в А.
Рассмотрим первую таблицу. Выберем все возможные варианты проезда из А в В и соответственно подсчитаем стоимости: AC(3) + CB(4); AC(3) + CE(2) + EB(2)
Примечание. В скобках указана стоимость проезда.
Стоимость, как первого, так и второго варианта маршрута равна 7.
Аналогично поступим для второй таблицы: AC(3) + CB(4); AE(1) + EC(2) + CB(4).
Как и в случае с предыдущей таблицей, стоимость как первого, так и второго варианта маршрута равна 7.
Выписываем все варианты для третьей таблицы: AC(3) + CB(4); AC(3) + CE(2) + EB(1).
Стоимость последнего варианта маршрута равна 6.
Ответ: таблица номер 3 содержит маршрут из А в В, стоимость которого не превышает 6.
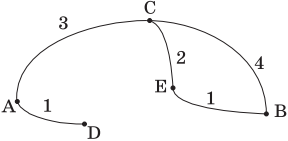
Пример 2. Для заданной информационной модели, записанной в форме таблицы, построить модель в виде схемы. В ячейках на пересечении строк и столбцов таблицы указана стоимость проезда между соседними станциями. Пустые ячейки означают, что станции не являются соседними.
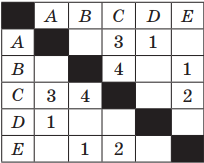
Решение. Отметим точку A, она должна быть соединена с C и D. Отмечаем точки C и D и соединяем их с точкой А дугами; над каждой дугой указываем стоимость проезда. Точка С должна быть соединена, кроме А, с точками В и Е. Точка D является соседней только с А. Точка В должна быть соединена, кроме С, с точкой Е. В результате можно получить следующую схему: