Закон всемирного тяготения. Сила тяжести
Закон всемирного тяготения
Закон всемирного тяготения (закон тяготения Ньютона) был открыт великим английским ученым Исааком Ньютоном в конце 60-х годов XVII века и опубликован в 1687 г. Он гласит:
Сила гравитационного притяжения двух тел с массами $m_1$ и $m_2$ прямо пропорциональна массе каждого из тел и обратно пропорциональна квадрату расстояния $r^2$ между ними:
$F=G{m_1m_2}/{r^2},$
где $G$ — гравитационная постоянная. Значение гравитационной постоянной было определено экспериментально в 1798 г. английским физиком Г. Кавендишем и составляет $6.67·10^{-11}H·м^2$/$кг^2$. Гравитацией (от лат. gravitas — тяжесть) называется притяжение всех тел во Вселенной друг к другу.
Закон всемирного тяготения имеет всеобъемлющий характер. Притяжение существует не только между Землей и телами, находящимися на ней. Все тела притягиваются друг к другу. Притягиваются между собой Земля и Луна. Притяжение Земли к Луне вызывает приливы и отливы воды. Огромные массы воды поднимаются в океанах и морях дважды в сутки на много метров. Земля и другие планеты движутся вокруг Солнца, притягиваясь друг к другу.
Необходимо помнить, что закон тяготения как всеобщий закон справедлив для материальных точек, и силы гравитационного взаимодействия направлены вдоль линии, соединяющей эти точки. Такие силы называются центральными.
При расчетах силы тяготения между двумя телами под расстоянием $г$ между ними имеется в виду расстояние между центрами тяжести этих тел. Это особенно важно в том случае, когда размеры тел сопоставимы с расстоянием между ними (тогда форма тела имеет значение). Как показывают расчеты, точные значения силы тяжести можно определить в следующих случаях:
- размеры тел пренебрежимо малы по сравнению с расстоянием между ними;
- имеются два однородных шара (произвольного размера);
- форма одного из тел — шар, а размеры и масса его тела намного больше, чем у второго тела (произвольной формы), которое находится вблизи поверхности первого.
Благодаря последнему случаю можно рассчитать силу притяжения к Земле любого предмета, находящегося на ней.
Сила тяжести
Сила, с которой Земля притягивает к себе тело, находящееся вблизи ее поверхности, называется силой тяжести.
То, что Земля притягивает к себе все тела, находящиеся на ее поверхности и вблизи нее (деревья, воду, дома, Луну и т. д.), или явление тяготения, следует из простых наблюдений за окружающим миром. Так, мяч, брошенный в горизонтальном направлении, через некоторое время оказывается на земле; камень, выпущенный из рук, падает вниз; прыгнувший вверх человек вскоре снова оказывается внизу. Благодаря явлению тяготения искусственный спутник, запущенный с Земли, летит не по прямой, а движется вокруг Земли.
Сила тяжести всегда направлена вертикально вниз, к центру Земли. Обозначается она обычно латинской буквой $F$ со значком «т» (тяжесть) внизу — $F_т$. Сила тяжести приложена к центру тяжести тела.
Центр тяжести тела произвольной формы находят так: подвешивают тело на нити за разные его точки. Точка пересечения всех направлений, отмеченных нитью, и будет центром тяжести тела. Для тел правильной формы центр тяжести находится в центре симметрии тела, и точка эта не обязательно принадлежит телу (например, центр симметрии кольца).
Сила тяжести для тела, находящегося вблизи поверхности Земли, равна:
$F_3=G{M_3m}/{R_3^2},$
где $M_3$ — масса Земли, $m$ — масса тела, $R_3$ — радиус Земли.
Согласно второму закону Ньютона, сила тяжести может быть определена как произведение массы тела на ускорение, которое в данном случае называется ускорением свободного падения $g$:
$F_т=mg$
Сопоставляя две последние формулы, получим выражение для ускорения свободного падения:
$g={GM_3}/{R_3^2}$
Таким образом, ускорение, с которым тело падает на Землю, — ускорение свободного падения — не зависит от массы тела, а также от других его характеристик (объема, плотности и т. д.)
Вблизи поверхности Земли оно составляет $9.8$ м/$с^2$.
Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся около полюсов, расположены немного ближе к центру Земли. В связи с этим сила тяжести на полюсе немного больше, чем на экваторе и других широтах (на экваторе $g = 9.78$ м/$с^2$, на Северном полюсе $g = 9.832$ м/$с^2$).
Сила тяжести, а значит, и ускорение свободного падения уменьшается при удалении от поверхности Земли. Для тела, находящегося на высоте $h$ над поверхностью Земли выражение для силы тяжести следует писать в виде:
$F_3=G{M_3m}/{(R_3+h)^2}$
Соответственно, для ускорения свободного падения:
$g=G{M_3}/{(R_3+h)^2}$
Из приведенной формулы следует, что лишь при подъеме на высоту $300$ км ускорение свободного падения уменьшается на $1$ м/$с^2$, т. е. всего на $10%$, а на высотах не только в несколько десятков или сотен метров, но и многих километров сила тяжести может считаться постоянной, не зависящей от положения тела. Именно благодаря этому свободное падение вблизи Земли можно считать равноускоренным движением.
Вес тела, невесомость, перегрузка
Вес — это сила, с которой любое тело вследствие притяжения Земли действует на опору или подвес.
Вес тела — векторная физическая величина, его обозначают буквой $Р$. Вес покоящегося, а также равномерно и прямолинейно движущегося (относительно Земли) тела по своему численному значению равен действующей на него силе тяжести:
$P=F_т=mg$
где $m$ — масса, $g$ — ускорение свободного падения.
Вес и сила тяжести приложены к разным телам, а именно: вес приложен к опоре или подвесу, а сила тяжести — к телу.
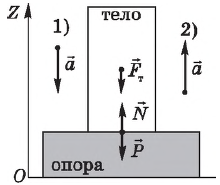
Вес и сила тяжести имеют разную физическую природу. Сила тяжести возникает вследствие взаимодействия тела и Земли. Вес тела возникает в результате взаимодействия тела и опоры (подвеса). Опора (подвес) и тело при этом деформируются, что приводит к появлению силы упругости. Из третьего закона Ньютона следует, что вес тела, т. е. сила, с которой тело давит на опору (или растягивает подвес), совпадает по величине с силой, действующей со стороны опоры на данное тело. Сила, с которой опора давит на находящееся на ней тело, называется силой реакции опоры. Обозначив силу реакции опоры через $N$, мы можем записать:
$P=N$
Полученная формула является более общей, чем $P=mg$, так как она остается справедливой и в том случае, когда тело вместе с опорой совершает ускоренное движение.
Вес тела не следует путать с его массой. Масса тела является скалярной величиной и измеряется в килограммах, а вес тела (как и любая другая сила) — векторная величина и измеряется в ньютонах.
Поскольку вес тела пропорционален ускорению свободного падения, которое различно на различных широтах, то вес тела зависит от географической широты и высоты местности (на полюсах вес несколько больше, чем на экваторе).
Вес можно измерять с помощью пружинных весов (динамометра).
Состояние невесомости — это состояние, в котором находится материальное тело, свободно движущееся в поле тяготения Земли (или другого небесного тела) под действием только сил тяготения. Отличительной особенностью такого состояния является отсутствие давления как на все тело в целом, так и на отдельные его части.
Рассмотрим условие достижения невесомости.
Если опора движется вместе с телом с ускорением а, направление которого совпадает с направлением ускорения свободного падения, то вес тела (определяемый из векторного уравнения $N↖{→}+{F_т}↖{→}=m{a}↖{→}$) в проекции на вертикальную ось $OZ$, направленную вверх, равен:
$P=N=m(g-a)$
Когда $g=a$, $P=0$, наступает невесомость.
При движении тела и опоры в направлении, противоположном направлению свободного падения, получим:
$P=N=m(g+a)$
В этом случае наступает перегрузка — вес тела увеличивается.
Движение небесных тел
Вокруг Солнца движутся девять больших планет. Все они удерживаются около Солнца силами тяготения. Эти силы очень велики. Например, между Солнцем и Землей действует сила тяготения, равная примерно $3⋅10^{22}Н$. Большое числовое значение этой силы объясняется тем, что массы Солнца и Земли очень велики.
Среди больших планет Солнечной системы наименьшую массу имеет Меркурий — его масса почти в $19$ раз меньше массы Земли. Вокруг многих планет движутся их спутники, которые также удерживаются вблизи планет силами тяготения. Спутник нашей Земли — Луна — самое близкое к нам небесное тело. Расстояние между Землей и Луной равно в среднем $380000$ км. Масса Луны в $81$ раз меньше массы Земли.
Чем меньше масса планеты, тем с меньшей силой она притягивает к себе тела. Сила тяжести на поверхности любой планеты рассчитывается по формуле:
$F_т=mg=GMm$/$R^2$
где $m$ — масса тела, $g$ — ускорение свободного падения на данной планете, $М$ — масса планеты, $R$ — радиус планеты, $G$ — гравитационная постоянная.
Космические скорости
Первая космическая скорость — это скорость, которую необходимо сообщить телу, чтобы оно стало искусственным спутником Земли, т. е. двигалось вокруг нее с постоянной скоростью по круговой орбите под действием силы тяжести.
Скорость эта определяется с учетом скорости равномерного движения по окружности и закона всемирного тяготения.
Центростремительное ускорение $а$ тела, равномерно движущегося по окружности, определяется выражением $a_n={υ^2}/{R}$. Поскольку в данном случае $а$ равно $g$ — ускорению свободного падения (т. к. тело движется в поле тяжести Земли), то, подставляя в $a_n={υ^2}/{R}$ вместо $а$ выражение для $g$ из $g=G{M_3}/{(R_3+h)^2}$, получим:
$υ=√{G{M_3}/{R_3+h}}$
Здесь $G$ — гравитационная постоянная, $М_3$ — масса Земли, $R_3$ — радиус Земли, $h$ — высота тела над поверхностью Земли. Это и есть формула круговой скорости спутника Земли. С такой скоростью движется спутник Земли по круговой орбите на высоте $h$ от поверхности Земли.
Пренебрегая $h$ по сравнению с $R$, получим:
$υ_1=√{G{M_3}/{R_3}}$
Это формула для расчета первой космической скорости при запуске спутника, т. е. той горизонтальной скорости, которую необходимо сообщить телу вблизи поверхности Земли, чтобы оно стало ее спутником. Запуск искусственного спутника осуществляется с помощью ракеты-носителя, которая поднимает тело спутника на высоту порядка $300$ км (это та высота, на которой уже почти не сказывается сопротивление атмосферы) и придает ему горизонтальную скорость $υ_1$. Спутник отделяется от ракеты-носителя и продолжает свое движение в гравитационном поле Земли. Численное значение первой космической скорости составляет $7.9$ км/с. Если придать телу большую скорость, оно будет двигаться по эллиптической орбите. По мере увеличения начальной скорости, придаваемой телу при запуске, орбита его будет вытягиваться, пока наконец не превратится в незамкнутую кривую — параболу.
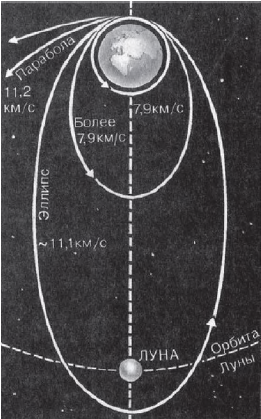
Вторая космическая (параболическая) скорость — это скорость, которую надо придать телу у поверхности Земли, чтобы оно ее покинуло, двигаясь по параболической траектории. Эта скорость в $√2$ раза больше первой космической: $υ_{II}=√2·υ_{I}=11.2$ км/с. При второй космической скорости тело покидает Землю, но остается в пределах Солнечной системы. Оно становится спутником Солнца.
Третья космическая скорость — это та наименьшая скорость, при которой тело, начиная движение вблизи поверхности Земли, покидает сначала Землю, а затем преодолевает притяжение Солнца, покидая Солнечную систему. Она равна $υ_{III}=16.7$ км/с.





