Равноускоренное движение, движение по окружности

Ускорение материальной точки

Ускорение — величина, характеризующая быстроту изменения скорости. Как правило, движение является неравномерным, т. е. происходит с переменной скоростью. На одних участках траектории тела могут иметь большую скорость, на других — меньшую. Например, поезд, отходящий от станции, со временем двигается все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.

Ускорение (или мгновенное ускорение) — векторная физическая величина, равная пределу отношения изменения скорости к промежутку времени, за который это изменение произошло, при стремлении $∆t$ к нулю, (т. е. производной $υ↖{→}$ по $t$):

$a↖{→}=lim↙{∆t→0}{∆υ↖{→}}/{∆t}=υ↖{→}_t'$

Составляющие $a↖{→} (а_х, а_у, а_z)$ равны соответственно:

$a_x=υ_x';a_y=υ_y';a_z=υ_z'$

Ускорение, как и изменение скорости, направлено в сторону вогнутости траектории и может быть разложено на две составляющие — тангенциальную — по касательной к траектории движения — и нормальную — перпендикулярно к траектории.

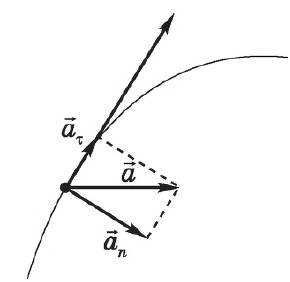
В соответствии с этим проекцию ускорения $а_х$ на касательную к траектории называют касательным, или тангенциальным ускорением, проекцию $a_n$ на нормаль — нормальным, или центростремительным ускорением.

Касательное ускорение определяет величину изменения численного значения скорости:

$a_t=lim↙{∆t→0}{∆υ}/{∆t}$

Нормальное, или центростремительное ускорение характеризует изменение направления скорости и определяется по формуле:

$a_n={v^2}/{R}$

где R — радиус кривизны траектории в соответствующей ее точке.

Модуль ускорения определяется по формуле:

$a=√{a_t^2+a_n^2}$

При прямолинейном движении полное ускорение $а$ равно тангенциальному $a=a_t$, т. к. центростремительное $a_n=0$.

Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с. Эту единицу обозначают 1 м/с² и называют «метр на секунду в квадрате».

Равноускоренное прямолинейное движение

Равноускоренным называется движение с постоянным ускорением ($a↖{→}=const$) при $a↖{→}↑↑υ↖{→}$. Когда вектор ускорения направлен против вектора скорости $a↖{→}↑↓υ↖{→}$, движение называется равнозамедленным.

Поскольку ускорение постоянно, оно равно изменению скорости за любой конечный интервал времени:

$a↖{→}={∆υ↖{→}}/{∆t}={υ↖{→}-{υ_0}↖{→}}/{∆t}$

При прямолинейном движении векторы $υ↖{→}$ и ${υ_0}↖{→}$, а следовательно, и вектор а направлены вдоль одной прямой, которая является траекторией движения. Вдоль этой же прямой удобно направить координатную ось X.

Тогда из последнего уравнения следует:

$a_x={∆υ_x}/{t}={υ_x-υ_{0x}}/{t}$

где $υ_{0x}$ — скорость в начальный момент времени, принятый за нуль; $υ_x$ — текущее значение скорости (в момент времени $t$). Формула для определения ускорения из состояния покоя (равноускоренное движение, начальная скорость равна нулю: $υ_{0x}=0$) имеет вид:

$a_x={υ_x}/{t}$

Если же нулю равна не начальная, а конечная скорость ($υ_x=0$, торможение при равнозамедленном движении), то формула ускорения принимает вид:

$a_x=-{υ_{0x}}/{t}$

Из формулы находим выражение для скорости при $υ_{0x}≠0$

$υ_x=υ_{0x}+a_{x}t$

Графики скорости при равноускоренном движении имеют вид прямых линий, наклон которых показывает, как быстро меняется скорость с течением времени. На рис. приведены графики для модуля скорости с ненулевой начальной скоростью для равноускоренного (II) и равнозамедленного (I) движений.

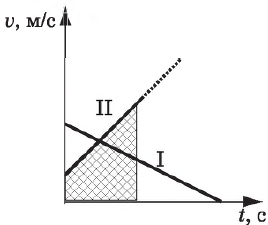
Путь, пройденный точкой за некоторое время $t$ (в данном случае совпадающий с перемещением $∆x↖{→}$ за то же время), легко определяется из рис.. Он равен площади трапеции, образованной графиком $υ(t)$, осями координат и прямой, восстановленной из заданной точки $t$ параллельно оси ординат. Аналитически эта площадь определяется, как известно, интегрированием функции $υ(t)$:

$∆x(t)=x(t)-x_0=∫↙{0}↖{t}υ(t)dt=∫↙{0}↖{t}(υ_0+at)dt=(υ_0t+{at^2}/{2})|↙{0}↖{t}=υ_0t+{at^2}/{2}$

Отсюда получаем закон прямолинейного равноускоренного движения:

$x=x_0+υ_0t+{at^2}/{2}$

Из этого уравнения при известных начальных условиях: координате тела в момент начала движения $х_0$, начальной скорости $υ_{0х}$, а также ускорению $а_х$ можно определить координату тела $х$ в любой момент времени $t$. В векторной форме:

$r↖{→}={r_0}↖{→}+{υ_0}↖{→}+{a↖{→}t^2}/{2}$

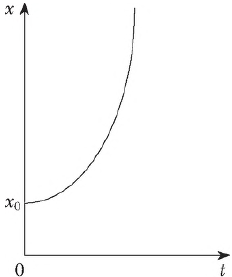
График зависимости координаты от времени прямолинейного равноускоренного движения представлен на рис.

Решая систему уравнений для двух точек траектории, соответствующих моментам времени $t_1$ и $t_2$, получим выражение, связывающее скорости тела в этих точках и ускорение с перемещением на участке $1→2$:

$υ_2^2-υ_1^2=2a(x_2-x_1)$

Эта формула часто бывает полезной при решении различных практических задач.

Равномерное движение точки по окружности

Наряду с равномерным прямолинейным движением очень часто приходится встречаться с равномерным движением по окружности. Такое движение могут совершать точки вращающихся колес, валов и роторов турбин, искусственные спутники, обращающиеся по круговым орбитам, и т. д. При равномерном движении по окружности численное значение скорости остается постоянным. Однако направление скорости при таком движении непрерывно изменяется.

В каждой точке круговой траектории скорость точки направлена по касательной к траектории в этой точке. В этом нетрудно убедиться, коснувшись вращающегося точильного камня, имеющего форму диска, стальным резцом: раскаленные частицы камня, имеющие в момент отрыва от него определенную скорость, будут отлетать от диска по касательной к нему. Эта скорость называется линейной скоростью вращения.

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот.

Известно, что при равномерном движении время определяется делением пройденного пути, т. е. длины окружности — $l_{окр}$, на скорость движения. Таким образом,

$T={l_{окр}}/{υ}={2πr}/{υ}.$

Величина, обратная периоду, называется частотой обращения и обозначается буквой $v$:

$v={1}/{T}$

Угловой скоростью точки $ω$ называется отношение угла поворота к интервалу времени, в течение которого этот поворот совершен:

$ω={φ}/{∆t}$

Угловая скорость выражается в радианах в секунду (рад/с).

Угловая скорость связана с периодом $Т$ и частотой $v$ вращения следующим соотношением:

$ω={2π}/{T}=2πv$

Центростремительное ускорение

Из-за непрерывного изменения направления скорости тело, движущееся по окружности, обладает ускорением. Это ускорение характеризует не быстроту изменения численного значения скорости (которое в данном случае не меняется), а быстроту изменения ее направления.

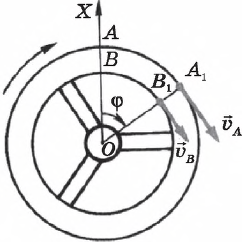
При равномерном движении по окружности ускорение тела все время направлено к ее центру и называется центростремительным ускорением. Чтобы найти его значение, рассмотрим отношение изменения вектора скорости $∆υ$ к малому интервалу времени $∆t$, за который это изменение произошло.

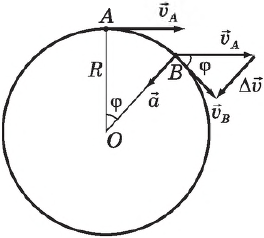
В силу малости угла $φ$ имеем:

$∆υ=υφ$

Так как угол $φ$ между векторами скорости в точках $А$ и $В$ равен углу $АОВ$ между радиусами, который, в свою очередь, равен отношению длины дуги $АВ$ к радиусу $R$, получим:

$φ={υ∆t}/{R}$

Из уравнений получим выражение для модуля вектора ускорения:

$a={∆υ}/{∆t}={υ^2}/{R}$

Из формул следует, что $a={4π^2R}/{T^2}$ и $a=4π^2Rv^2$

Поступательное и вращательное движение твердого тела

Поступательное движение — это движение твердого тела, при котором прямая, соединяющая две любые точки тела, перемещается параллельно своему начальному направлению.

При поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю направления скорости и ускорения.

Поступательное движение может быть как криволинейным, так и прямолинейным. Например, поступательно движется кабина колеса обозрения. Человек, стоящий на ступеньке движущегося эскалатора, также движется поступательно. Для описания его движения (т. е. определения изменения скорости со временем, пути) достаточно рассмотреть движение только одной его точки.

Другими словами, изучение поступательного движения твердого тела сводится к задаче кинематики точки.

Вращательное движение абсолютно твердого тела вокруг неподвижной оси — один из самых простых (после поступательного) видов движения. Оно характеризуется углом поворота точек тела вокруг оси $O_1O_2$, жестко связанной с телом.

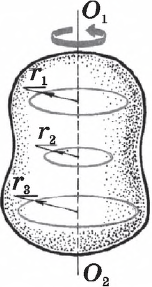
Угол поворота $φ$ отсчитывается между двумя лучами, выходящими из одной точки на оси $O_1O_2$ и перпендикулярными к ней: один из лучей (ОХ) неподвижен, другой (ОА) жестко связан с телом.

При вращении тела вокруг неподвижной оси все его точки поворачиваются на одинаковый угол, но описывают окружности разных радиусов в зависимости от степени удаленности точки тела от оси вращения.

Равномерное вращение твердого тела или точки его окружности характеризуется постоянной угловой скоростью.

При равномерном вращении, если известна угловая скорость в начальный момент времени $t_0=0$, можно определить угол поворота тела за время $t$ и тем самым положение точек тела:

$φ=ωt$

При ненулевом значении угла поворота $φ_0$ в начальный момент времени ($t=0$) закон вращательного движения описывается уравнением:

$φ=φ_0+ωt$

Связь между линейной $υ$ и угловой $ω$ скоростями и центростремительным ускорением $а$ определяется соотношениями:

$υ={2πR}/{T}=2πRv; υ=ωR; a={υ^2}/{R}=ω^2R$