Пружинный и математический маятник
Свободные колебания математического и пружинного маятников
Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий.
Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.
Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется колебательной системой.
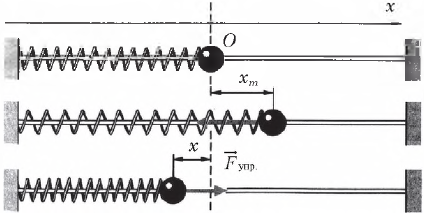
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины, входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.
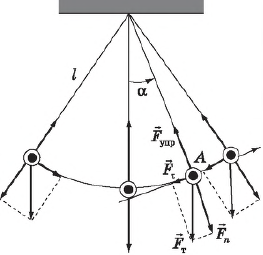
Другим классическим примером механической колебательной системы является математический маятник. В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия. Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называются силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свободные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.
Условиями возникновения свободных колебаний являются:
- возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;
- отсутствие трения в системе.
Динамика свободных колебаний
Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости $F_{упр}$ может быть получено с учетом второго закона Ньютона ($F=ma$) и закона Гука ($F_{упр}=-kx$), где $m$ — масса шарика, $а$ — ускорение, приобретаемое шариком под действием силы упругости, $k$ — коэффициент жесткости пружины, $х$ — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось $Ох$). Приравнивая правые части этих уравнений и учитывая, что ускорение $а$ — это вторая производная от координаты $х$ (смещения), получим:
$x''=-{k}/{m}x$
Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени {ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.
Колебания математического маятника. Для получения уравнения колебания математического маятника необходимо разложить силу тяжести $F_т=mg$ на нормальную $F_n$ (направленную вдоль нити) и тангенциальную $F_τ$ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести $F_n$ и сила упругости нити $F_{упр}$ в сумме сообщают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меняющее ее направление, а тангенциальная составляющая $F_τ$ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускорения — $ma_τ=F_τ$ и учитывая, что $F_τ=-mgsinα$, получим:
$a_τ=-gsinα$
Знак минус появился потому, что сила и угол отклонения от положения равновесия $α$ имеют противоположные знаки. Для малых углов отклонения $sinα≈α$. В свою очередь, $α={s}/{l}$, где $s$ — дуга $ОА$, $l$ — длина нити. Учитывая, что $a_τ=s''$, окончательно получим:
$s''={g}/{l}s$
Вид уравнения $s''={g}/{l}s$ аналогичен уравнению $x''=-{k}/{m}x$. Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).
Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.
Решением уравнений $x''=-{k}/{m}x$ и $s''={g}/{l}s$ является функция вида:
$x=x_{m}cosω_{0}t$(или $x=x_{m}sinω_{0}t$)
То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими.
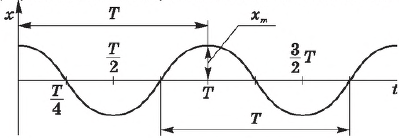
В уравнении $x=x_{m}cosω_{0}t$ хт— амплитуда колебания, $ω_{0}$ — собственная циклическая (круговая) частота колебаний.
Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:
$ω_0=√{{k}/{m}}; T=2π√{{m}/{k}}$
Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.
Для математического маятника выполняются равенства:
$ω_0=√{{g}/{l}}; T=2π√{{l}/{g}}$
Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).
Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.
Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятника, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.
Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции $x=x_{m}cosω_{0}t$, получим выражение для скорости:
$x'=υ=-x_{m}·sinω_{0}t=υ_{m}cos(ω_{0}t+{π}/{2})$
где $υ_{m}$ — амплитуда скорости.
Аналогично выражение для ускорения а получим, дифференцируя $x'=υ=-x_{m}·sinω_{0}t=υ_{m}cos(ω_{0}t+{π}/{2})$:
$a=x''=υ'-x_{m}ω_0^{2}cosω_{0}t=a_{m}·cos(ω_{0}t+π)$
где $a_m$ — амплитуда ускорения. Таким образом, из полученных уравнений следует, что амплитуда скорости гармонических колебаний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания:
$υ_{m}=ω_{0}x_m; a_m=ω_0^{2}x_m$





