Влажность воздуха
Насыщенные и ненасыщенные пары
Насыщенный пар
При испарении одновременно с переходом молекул из жидкости в пар происходит и обратный процесс. Беспорядочно двигаясь над поверхностью жидкости, часть молекул, покинувших ее, снова возвращается в жидкость.
Если испарение происходит в закрытом сосуде, то сначала число молекул, вылетевших из жидкости, будет больше числа молекул, возвратившихся обратно в жидкость. Поэтому плотность пара в сосуде будет постепенно увеличиваться. С увеличением плотности пара увеличивается и число молекул, возвращающихся в жидкость. Довольно скоро число молекул, вылетающих из жидкости, станет равным числу молекул пара, возвращающихся обратно в жидкость. С этого момента число молекул пара над жидкостью будет постоянным. Для воды при комнатной температуре это число приблизительно равно $10^{22}$ молекул за $1с$ на $1см^2$ площади поверхности. Наступает так называемое динамическое равновесие между паром и жидкостью.
Пар, находящийся в динамическом равновесии со своей жидкостью, называется насыщенным паром.
Это означает, что в данном объеме при данной температуре не может находиться большее количество пара.
При динамическом равновесии масса жидкости в закрытом сосуде не изменяется, хотя жидкость продолжает испаряться. Точно так же не изменяется и масса насыщенного пара над этой жидкостью, хотя пар продолжает конденсироваться.
Давление насыщенного пара. При сжатии насыщенного пара, температура которого поддерживается постоянной, равновесие сначала начнет нарушаться: плотность пара возрастет, и вследствие этого из газа в жидкость будет переходить больше молекул, чем из жидкости в газ; продолжаться это будет до тех пор, пока концентрация пара в новом объеме не станет прежней, соответствующей концентрации насыщенного пара при данной температуре (и равновесие восстановится). Объясняется это тем, что число молекул, покидающих жидкость за единицу времени, зависит только от температуры.
Итак, концентрация молекул насыщенного пара при постоянной температуре не зависит от его объема.
Поскольку давление газа пропорционально концентрации его молекул, то и давление насыщенного пара не зависит от занимаемого им объема. Давление $р_0$, при котором жидкость находится в равновесии со своим паром, называют давлением насыщенного пара.
При сжатии насыщенного пара большая его часть переходит в жидкое состояние. Жидкость занимает меньший объем, чем пар той же массы. В результате объем пара при неизменной его плотности уменьшается.
Зависимость давления насыщенного пара от температуры. Для идеального газа справедлива линейная зависимость давления от температуры при постоянном объеме. Применительно к насыщенному пару с давлением $р_0$ эта зависимость выражается равенством:
$p_0=nkT$
Так как давление насыщенного пара не зависит от объема, то, следовательно, оно зависит только от температуры.
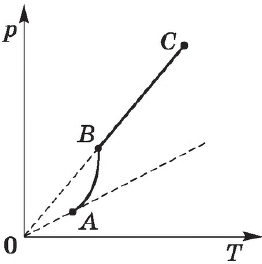
Экспериментально определенная зависимость $Р_0(Т)$ отличается от зависимости $p_0=nkT$ для идеального газа. С увеличением температуры давление насыщенного пара растет быстрее, чем давление идеального газа (участок кривой $АВ$). Это становится особенно очевидным, если провести изохору через точку $А$ (пунктирная прямая). Происходит это потому, что при нагревании жидкости часть ее превращается в пар, и плотность пара растет.
Поэтому, согласно формуле $p_0=nkT$, давление насыщенного пара растет не только в результате повышения температуры жидкости, но и вследствие увеличения концентрации молекул (плотности) пара. Главное различие в поведении идеального газа и насыщенного пара заключается в изменении массы пара при изменении температуры при неизменном объеме (в закрытом сосуде) или при изменении объема при постоянной температуре. С идеальным газом ничего подобного происходить не может (МКТ идеального газа не предусматривает фазового перехода газа в жидкость).
После испарения всей жидкости поведение пара будет соответствовать поведению идеального газа (участок $ВС$ кривой).
Ненасыщенный пар
Если в пространстве, содержащем пары какой-либо жидкости, может происходить дальнейшее испарение этой жидкости, то пар, находящийся в этом пространстве, является ненасыщенным.
Пар, не находящийся в состоянии равновесия со своей жидкостью, называется ненасыщенным.
Ненасыщенный пар можно простым сжатием превратить в жидкость. Как только это превращение началось, пар, находящийся в равновесии с жидкостью, становится насыщенным.
Влажность воздуха
Влажность воздуха — это содержание в воздухе водяного пара.
Окружающий нас атмосферный воздух вследствие непрерывного испарения воды с поверхности океанов, морей, водоемов, влажной почвы и растений всегда содержит в себе водяные пары. Чем больше водяных паров находится в определенном объеме воздуха, тем ближе пар к состоянию насыщения. С другой стороны, чем выше температура воздуха, тем большее количество водяных паров требуется для его насыщения.
В зависимости от количества водяных паров, находящихся при данной температуре в атмосфере, воздух бывает различной степени влажности.
Количественная оценка влажности
Для того чтобы количественно оценить влажность воздуха, пользуются, в частности, понятиями абсолютной и относительной влажности.
Абсолютная влажность — это количество граммов водяного пара, содержащееся в $1м^3$ воздуха при данных условиях, т. е. это плотность водяного пара $р$, выраженная в г/$м^3$.
Относительная влажность воздуха $φ$ — это отношение абсолютной влажности воздуха $р$ к плотности $р_0$ насыщенного пара при той же температуре.
Относительную влажность выражают в процентах:
$φ=({p}/{p_0})·100%$
Концентрация пара связана с давлением ($p_0=nkT$), поэтому относительную влажность можно определить как процентное отношение парциального давления $р$ пара в воздухе к давлению $р_0$ насыщенного пара при той же температуре:
$φ=({p}/{p_0})·100%$
Под парциальным давлением понимают давление водяного пара, которое он производил бы, если бы все другие газы в атмосферном воздухе отсутствовали.
Если влажный воздух охлаждать, то при некоторой температуре находящийся в нем пар можно довести до насыщения. При дальнейшем охлаждении водяной пар начнет конденсироваться в виде росы.
Точка росы
Точка росы — это температура, до которой должен охладиться воздух, чтобы находящийся в нем водяной пар достиг состояния насыщения при постоянном давлении и данной влажности воздуха. При достижении точки росы в воздухе или на предметах, с которыми он соприкасается, начинается конденсация водяного пара. Точка росы может быть вычислена по значениям температуры и влажности воздуха или определена непосредственно конденсационным гигрометром. При относительной влажности воздуха $φ = 100%$ точка росы совпадает с температурой воздуха. При $φ < 100%$ точка росы всегда ниже температуры воздуха. Так, при температуре воздуха $15°$С и относительной влажности $(%) 100, 80, 60, 40$ точка росы оказывается равной $15.0; 11.6; 7.3; 1.5°$С.





